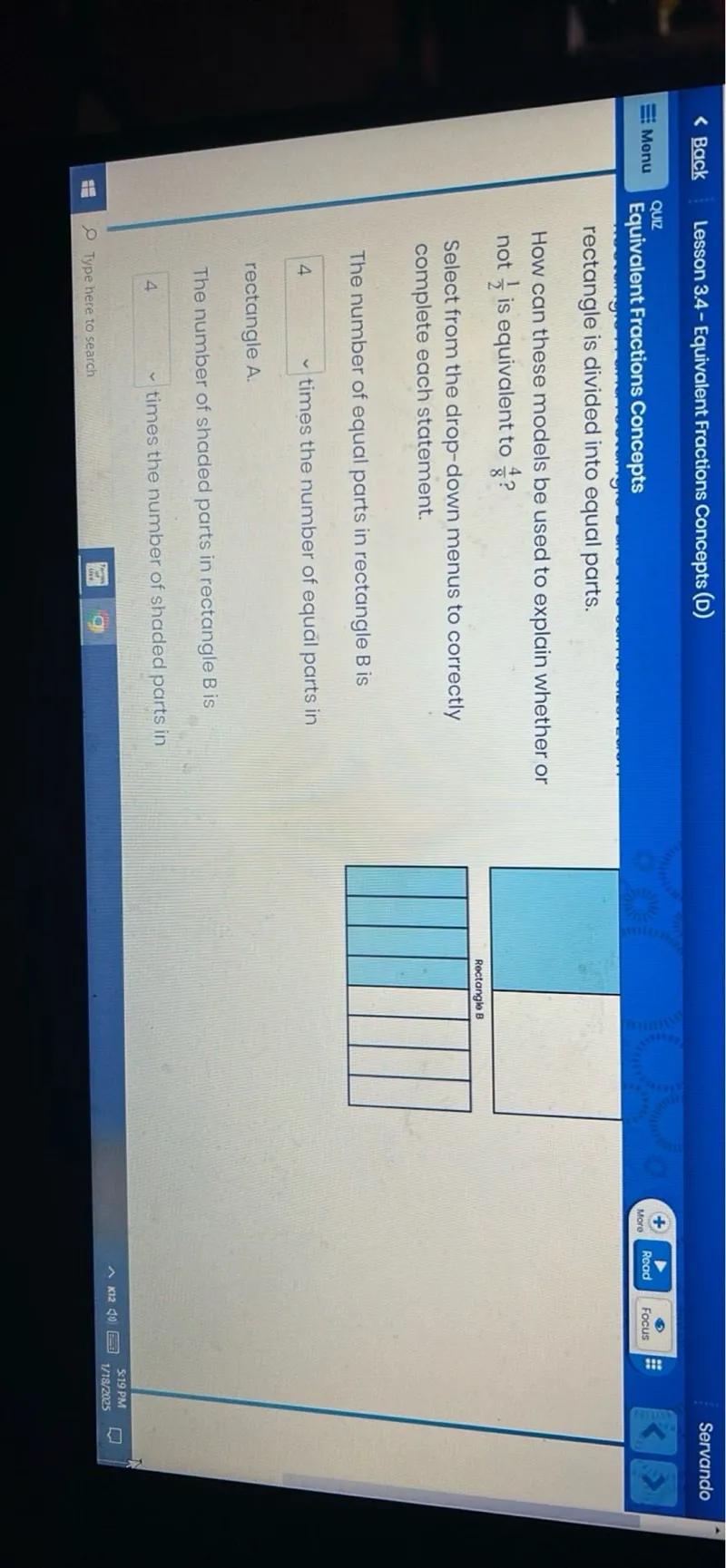
Questions: Equivalent Fractions Concepts How can these models be used to explain whether or not 1/2 is equivalent to 4/8? Select from the drop-down menus to correctly complete each statement. The number of equal parts in rectangle B is □ Rectangle B □ times the number of equal parts in rectangle A. The number of shaded parts in rectangle B is □ 4 times the number of shaded parts in
Transcript text: Equivalent Fractions Concepts
How can these models be used to explain whether or not $\frac{1}{2}$ is equivalent to $\frac{4}{8}$ ?
Select from the drop-down menus to correctly complete each statement.
The number of equal parts in rectangle $B$ is
$\square$
Rectangle B
\begin{tabular}{|l|l|l|l|l|l|l|l|}
\hline & & & & & & & \\
\hline
\end{tabular}
$\square$ times the number of equal parts in rectangle A .
The number of shaded parts in rectangle $B$ is
$\square$
4 times the number of shaded parts in
Solution
Was this solution helpful?
Answered
