Questions: Consider Abdul and Bridget's production functions: Abdul's catch: y^A = h^A(α - β(h^A + h^B)) Bridget's catch: y^B = h^B(α - β(h^A + h^B)) Select the SIX correct statements The higher the value of the parameter, the more fishes Bridget can catch in an hour. If Abdul fishes zero hours and Bridget fishes 10 hours, Bridget will catch 10β fishes. These production functions tell us that both Abdul and Bridget experience increasing marginal disutility of effort. These production functions indicate interdependence between Abdul and Bridget. If Abdul fishes zero hours and Bridget fishes 10 hours, Bridget will catch 10α - 100β fishes. These production functions indicate that fishing is subject to 'decreasing productivity'; These production functions convey the information that there is an externality in this game. These production functions involve no externality, indicating that this is likely to be an 'Invisible Hand' game. If Abdul fishes five hours and Bridget fishes 10 hours, Bridget will catch 10α fishes. As Bridget's fishing hours increase, everything else remaining constant, the number of fishes Abdul can catch increases. As Bridget's fishing hours increase, everything else remaining constant, the number of fishes Abdul can catch decreases.
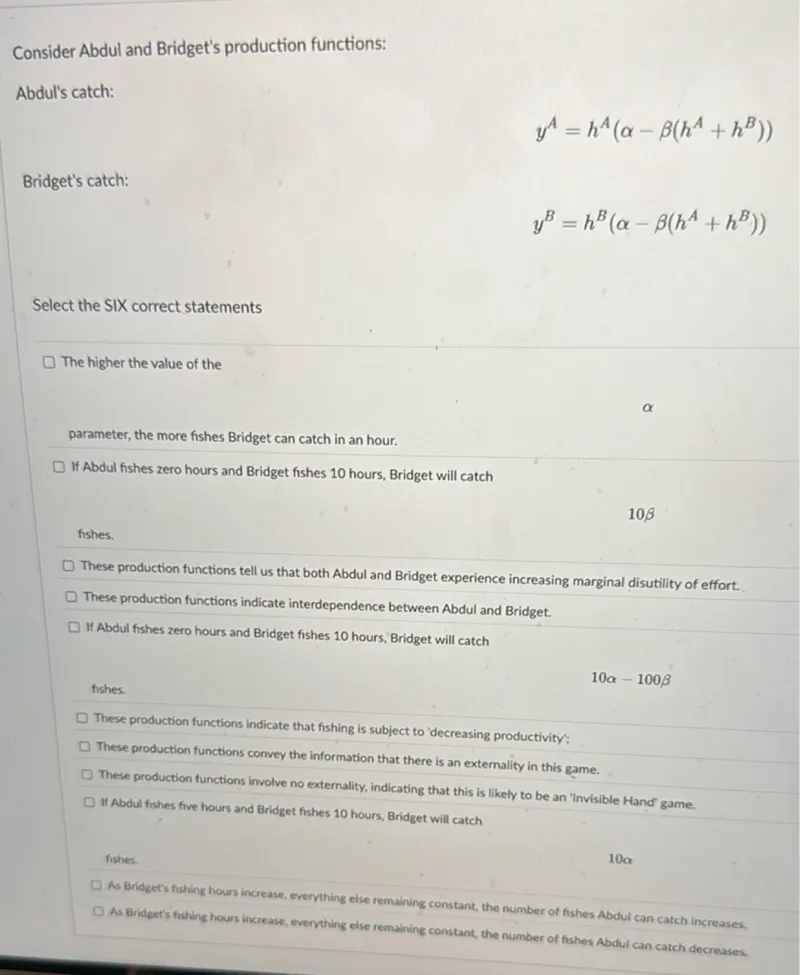
Transcript text: Consider Abdul and Bridget's production functions:
Abdul's catch:
\[
y^{A}=h^{A}\left(\alpha-\beta\left(h^{A}+h^{B}\right)\right)
\]
Bridget's catch:
\[
y^{B}=h^{B}\left(\alpha-\beta\left(h^{A}+h^{B}\right)\right)
\]
Select the SIX correct statements
The higher the value of the parameter, the more fishes Bridget can catch in an hour.
If Abdul fishes zero hours and Bridget fishes 10 hours, Bridget will catch $10 \beta$ fishes.
These production functions tell us that both Abdul and Bridget experience increasing marginal disutility of effort.
These production functions indicate interdependence between Abdul and Bridget.
If Abdul fishes zero hours and Bridget fishes 10 hours, Bridget will catch
\[
10 \alpha-100 \beta
\]
fishes.
These production functions indicate that fishing is subject to 'decreasing productivity';
These production functions convey the information that there is an externality in this game.
These production functions involve no externality, indicating that this is likely to be an 'Invisible Hand' game.
If Abdul fishes five hours and Bridget fishes 10 hours, Bridget will catch $10 \alpha$ fishes.
As Bridget's fishing hours increase, everything else remaining constant, the number of fishes Abdul can catch increases.
As Bridget's fishing hours increase, everything else remaining constant, the number of fishes Abdul can catch decreases.





