Questions: Use the Pythagorean Theorem and the square root property to solve the following problem. Express your answer in simplified radical form. Then find a decimal approximation to the nearest tenth. A rectangular park is 30 miles long and 10 miles wide. How long is a pedestrian route that runs diagonally across the park? In simplified radical form, the pedestrian route is miles long Rounded to the nearest tenth, the pedestrian route is miles long
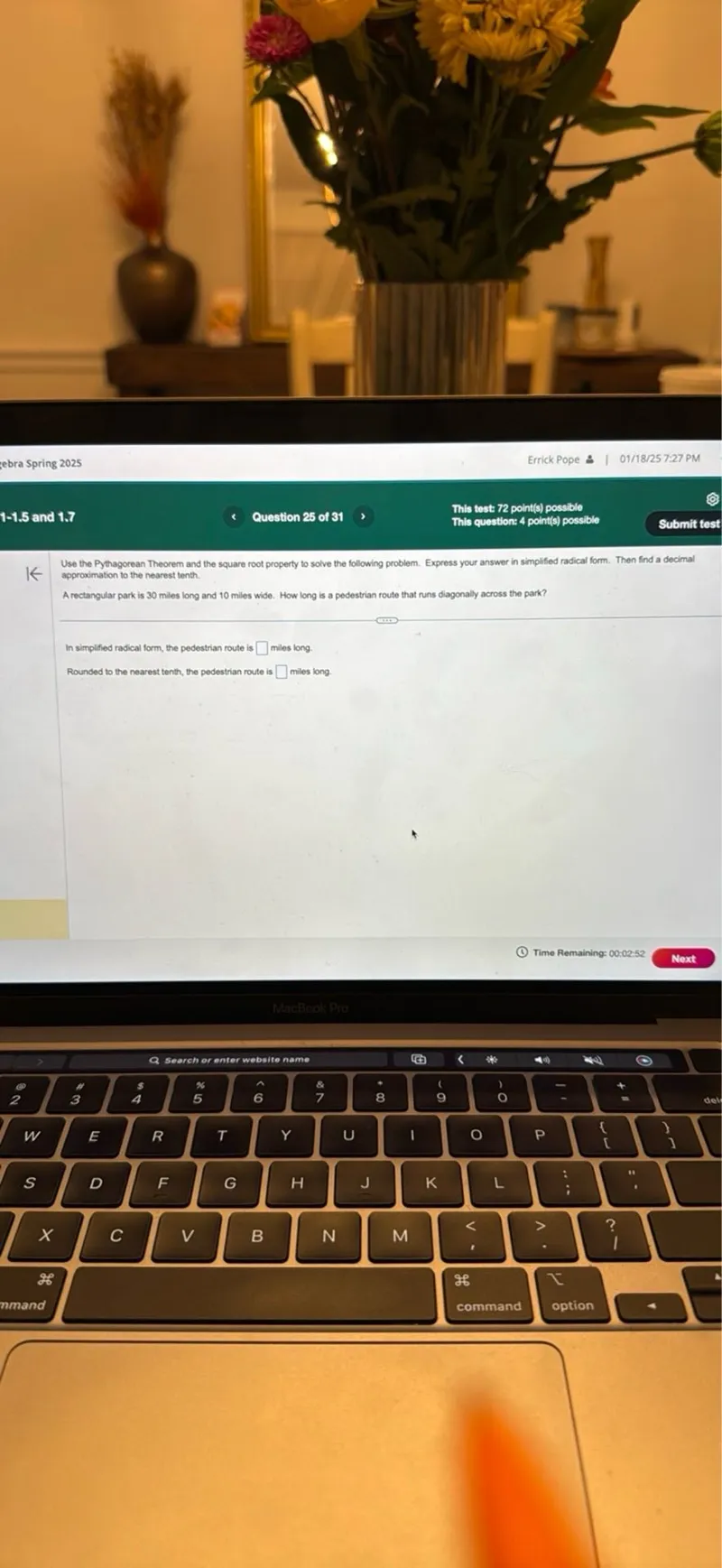
Transcript text: Use the Pythagorean Theorem and the square root property to solve the following problem. Express your answer in simplified radical form. Then find a decimal approximation to the nearest tenth.
A rectangular park is 30 miles long and 10 miles wide. How long is a pedestrian route that runs diagonally across the park?
In simplified radical form, the pedestrian route is $\square$ miles long
Rounded to the nearest tenth, the pedestrian route is $\square$ miles long





