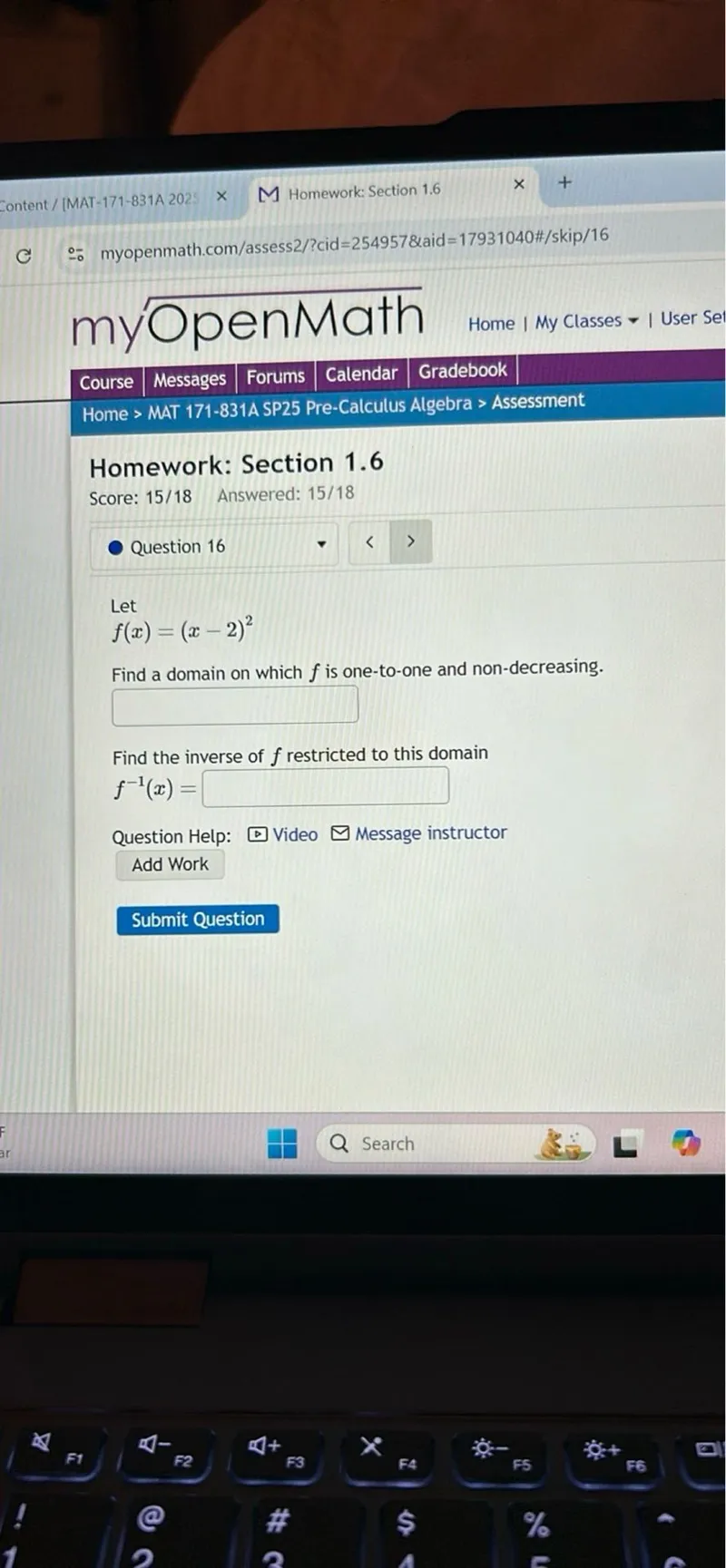
Questions: Let f(x) = (x-2)^2 Find a domain on which f is one-to-one and non-decreasing. Find the inverse of f restricted to this domain f^(-1)(x) =

Find a domain on which \( f(x) = (x-2)^2 \) is one-to-one and non-decreasing.

Identify the interval for non-decreasing behavior.

The function \( f(x) \) is a parabola that opens upwards, and it is non-decreasing on the interval \([2, \infty)\).

\(\boxed{[2, \infty)}\)

Find the inverse of \( f \) restricted to the domain \([2, \infty)\).

Set up the equation to find the inverse.

We start with \( y = (x-2)^2 \) and solve for \( x \).

Solve for \( x \) in terms of \( y \).

The solution gives \( x = \sqrt{y} + 2 \) for \( y \geq 0 \).

\(\boxed{f^{-1}(x) = \sqrt{x} + 2}\)

The domain on which \( f \) is one-to-one and non-decreasing is \([2, \infty)\).
The inverse of \( f \) restricted to this domain is \( f^{-1}(x) = \sqrt{x} + 2 \).