Questions: In right triangle XYZ, angle X and angle Z are complementary angles and cos(X) is 9/11. What is sin(Z) ? A. 11/9 B. 9/11 C. sqrt(20)/9 D. sqrt(20)/11

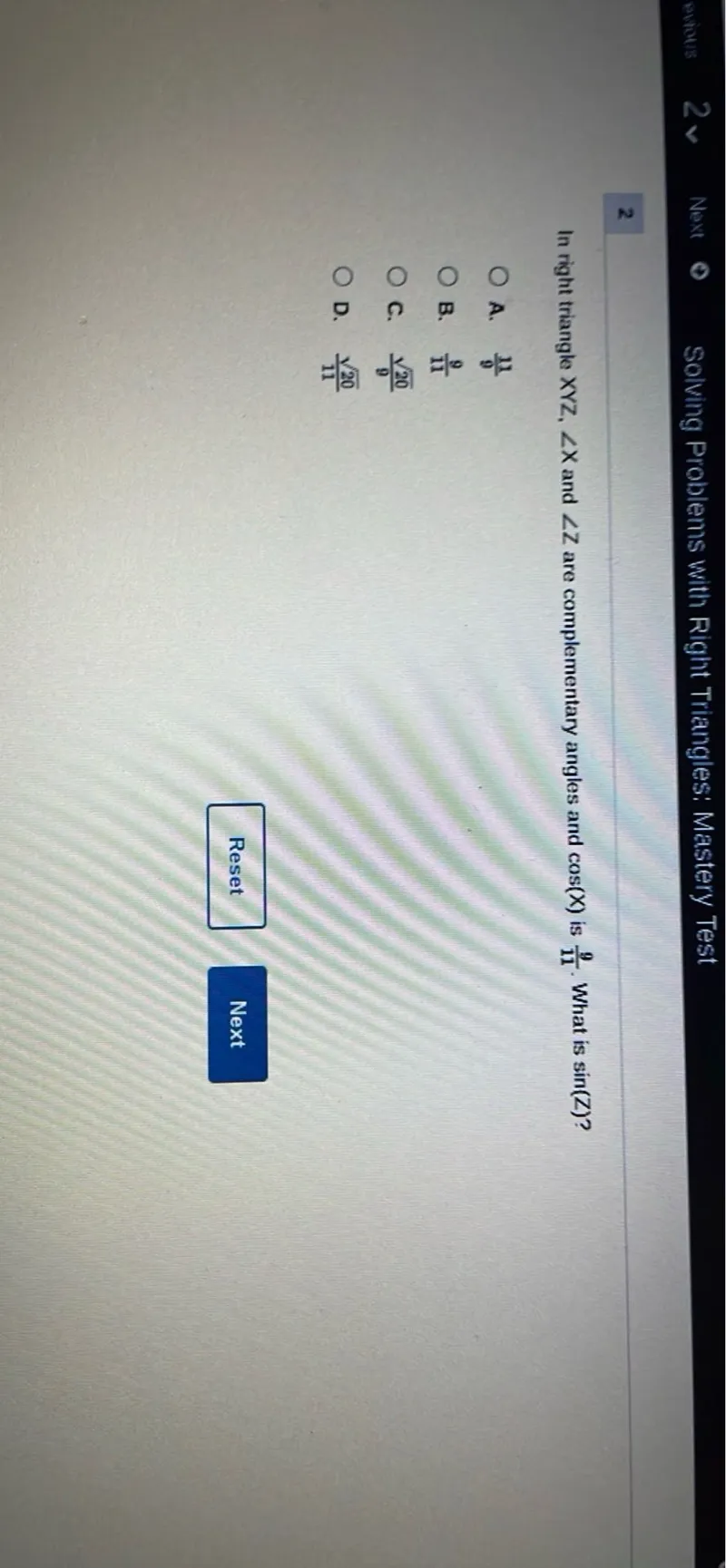
Find \(\sin(Z)\) in the right triangle \(XYZ\) where \(\angle X\) and \(\angle Z\) are complementary angles and \(\cos(X) = \frac{9}{11}\).

Understand the relationship between \(\angle X\) and \(\angle Z\).

Since \(\angle X\) and \(\angle Z\) are complementary angles in a right triangle, \(\angle X + \angle Z = 90^\circ\). This means \(\angle Z = 90^\circ - \angle X\).

Use the complementary angle identity for sine and cosine.

The identity \(\sin(90^\circ - \theta) = \cos(\theta)\) applies here. Therefore, \(\sin(Z) = \sin(90^\circ - \angle X) = \cos(\angle X)\).

Substitute the given value of \(\cos(\angle X)\).

Given \(\cos(\angle X) = \frac{9}{11}\), we substitute this into the identity: \(\sin(Z) = \frac{9}{11}\).

\(\boxed{\sin(Z) = \frac{9}{11}}\)

The value of \(\sin(Z)\) is \(\boxed{\frac{9}{11}}\).
The answer is B.