Questions: Solve each system by graphing. 5) y=x+3, 2x+4y=4 6) y=2x+1 7) x+2y+4=2x-4y=22 8) 2x-y=4, 4x=2y+8
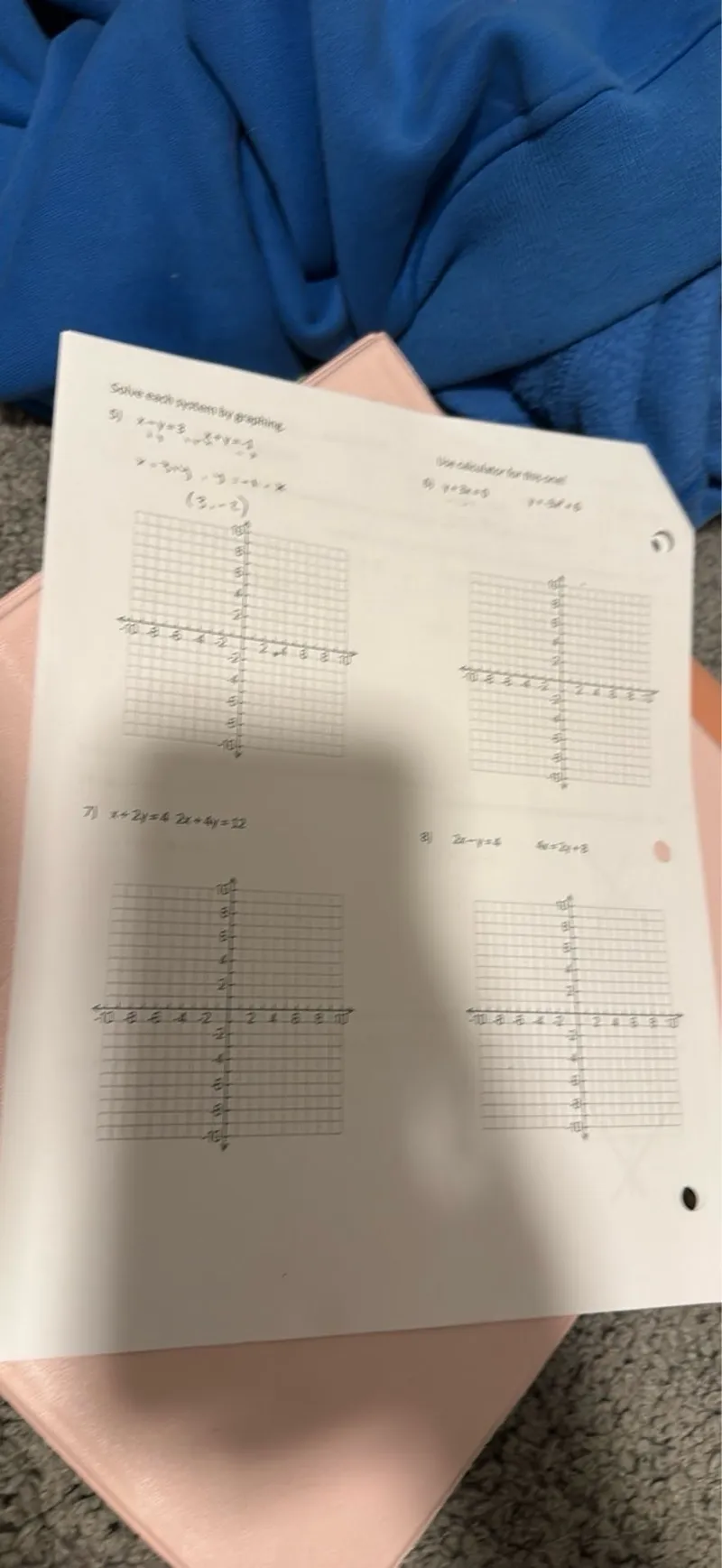
Transcript text: Solve each system by graphing.
5) $y=x+3$, $2x+4y=4$
6) $y=2x+1$
7) $x+2y+4=2x-4y=22$
8) $2x-y=4$, $4x=2y+8$





