Questions: Hana wrote the following inequality: 3x + 2 ≤ 5(x - 4) What is the solution set to the inequality she wrote? A. x ≤ 3 B. x ≥ 3 C. x ≤ -11 D. x ≥ 11

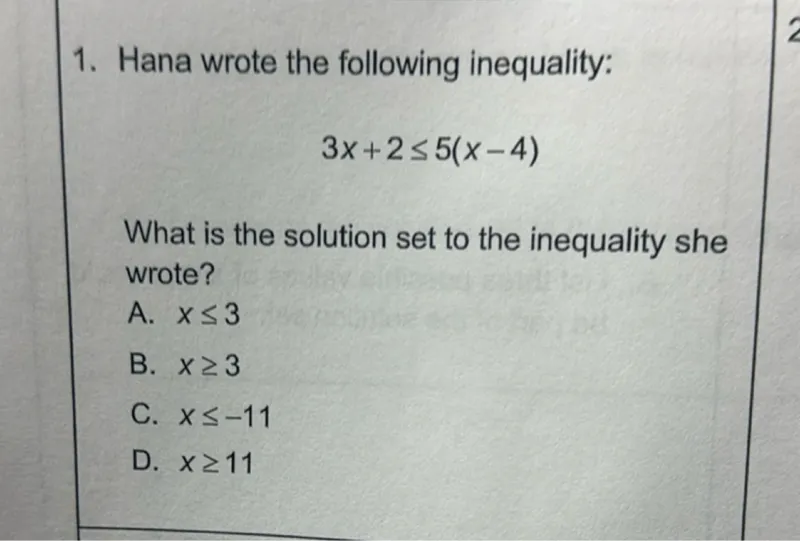
Hana wrote the following inequality: 3x + 2 ≤ 5(x - 4) What is the solution set to the inequality she wrote? A. x ≤ 3 B. x ≥ 3 C. x ≤ -11 D. x ≥ 11
Transcript text: 1. Hana wrote the following inequality: \[ 3 x+2 \leq 5(x-4) \] What is the solution set to the inequality she wrote? A. $x \leq 3$ B. $x \geq 3$ C. $x \leq-11$ D. $x \geq 11$
failed

Solution

failed
failed

Solution Steps

Step 1: Distribute and Simplify the Right Side

Start by distributing the \(5\) on the right side of the inequality:

\[ 3x + 2 \leq 5(x - 4) \implies 3x + 2 \leq 5x - 20 \]

Step 2: Move Terms Involving \(x\) to One Side

Subtract \(3x\) from both sides to get all terms involving \(x\) on one side:

\[ 2 \leq 5x - 3x - 20 \implies 2 \leq 2x - 20 \]

Step 3: Isolate the Variable

Add \(20\) to both sides to isolate the term with \(x\):

\[ 2 + 20 \leq 2x \implies 22 \leq 2x \]

Divide both sides by \(2\) to solve for \(x\):

\[ \frac{22}{2} \leq x \implies 11 \leq x \]

This can be rewritten as:

\[ x \geq 11 \]

Final Answer

The solution set to the inequality is:

\[ \boxed{x \geq 11} \]

Thus, the correct answer is D.

Was this solution helpful?
failed
Unhelpful
failed
Helpful

Questions asked by other users

failedAnswered
Which element is in the same group as Chlorine? Al - Aluminum Br - Bromine Kr - Krypton Ne - Neon
failedAnswered
A common disease or disorder of the circulatory system is a heart attack, which is also known as: A) Coronary occlusion B) Myocardial infarction C) Arteriosclerosis D) Anemia
failedAnswered
Professor Ivy records the following scores on her final: 35, 48, 48, 52, 69, 72, 81, 88, 92. What is the median score for the final?
failedAnswered
uestion 6 of 11 Which response would the nurse provide when asked by a pregnant patient with newly diagnosed varicose veins how to prevent more from developing? "Be sure to rest often in a sitting position." "The varicose veins will disappear after you have given birth." "Wear graduated compression stockings and frequently elevate your legs." "These will have to be removed during a surgical procedure to prevent further spread." NOT SURE CONFIDENT Search
failedAnswered
Which statement correctly describes the relationship between reactant and yield? The actual yield is calculated from the amount of the excess reactant present. The actual yield is calculated from the amount of the limiting reactant present. The theoretical yield is calculated from the amount of the excess reactant present The theoretical yield is calculated from the amount of the limiting reactant present.