Questions: Suppose H(x)=(9-4x)^7. Find two functions f and g such that (f∘g)(x)=H(x). Neither function can be the identity function. (There may be more than one correct answer.) f(x)= g(x)=

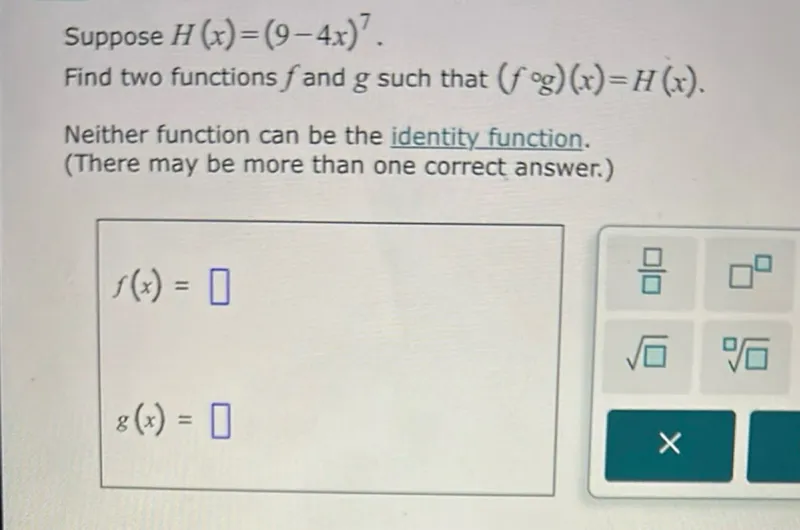
Suppose H(x)=(9-4x)^7.
Find two functions f and g such that (f∘g)(x)=H(x).
Neither function can be the identity function.
(There may be more than one correct answer.)
f(x)=
g(x)=

Transcript text: Suppose $H(x)=(9-4 x)^{7}$. Find two functions $f$ and $g$ such that $(f \circ g)(x)=H(x)$. Neither function can be the identity function. (There may be more than one correct answer.) \[ f(x)= \] \[ g(x)= \]

Solution

Solution Steps

Step 1: Understand the composition of functions

We are given $ H(x) = (9 - 4x)^7 $. We need to find two functions $ f $ and $ g $ such that $ (f \circ g)(x) = H(x) $, where neither $ f $ nor $ g $ is the identity function.

Step 2: Break down $ H(x) $ into simpler functions

The function $ H(x) $ can be thought of as a composition of two functions:

A function $ g(x) $ that takes $ x $ and produces $ 9 - 4x $.
A function $ f(x) $ that takes the output of $ g(x) $ and raises it to the 7th power.

Step 3: Define $ g(x) $ and $ f(x) $

Let $ g(x) = 9 - 4x $. This function is not the identity function because it involves a linear transformation of $ x $.

Let $ f(x) = x^7 $. This function is not the identity function because it involves raising $ x $ to the 7th power.

Step 4: Verify the composition

Now, verify that $ (f \circ g)(x) = H(x) $: \[ (f \circ g)(x) = f(g(x)) = f(9 - 4x) = (9 - 4x)^7 = H(x). \] This confirms that the functions $ f(x) = x^7 $ and $ g(x) = 9 - 4x $ satisfy the condition $ (f \circ g)(x) = H(x) $.

\[ f(x) = x^7 \] \[ g(x) = 9 - 4x \]