Questions: Step 1: ABCD is a parallelogram Step 2: ∠CDA ≅ ∠BAD, ∠CAD ≅ ∠BDA Step 3: Reflexive Property Step 4: △CIDA ≅ △BAD
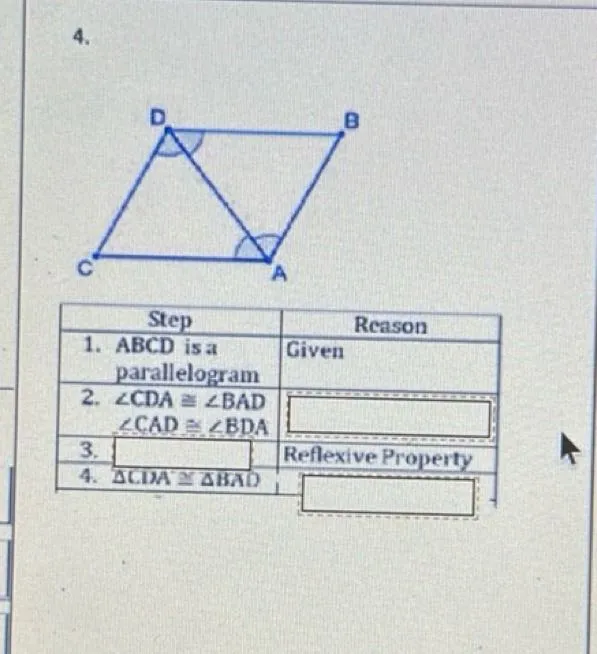
Transcript text: Step 1: ABCD is a parallelogram
Step 2: ∠CDA ≅ ∠BAD, ∠CAD ≅ ∠BDA
Step 3: Reflexive Property
Step 4: △CIDA ≅ △BAD





