a) Check the conditions.
i) Is the independence condition satisfied? Why or why not?
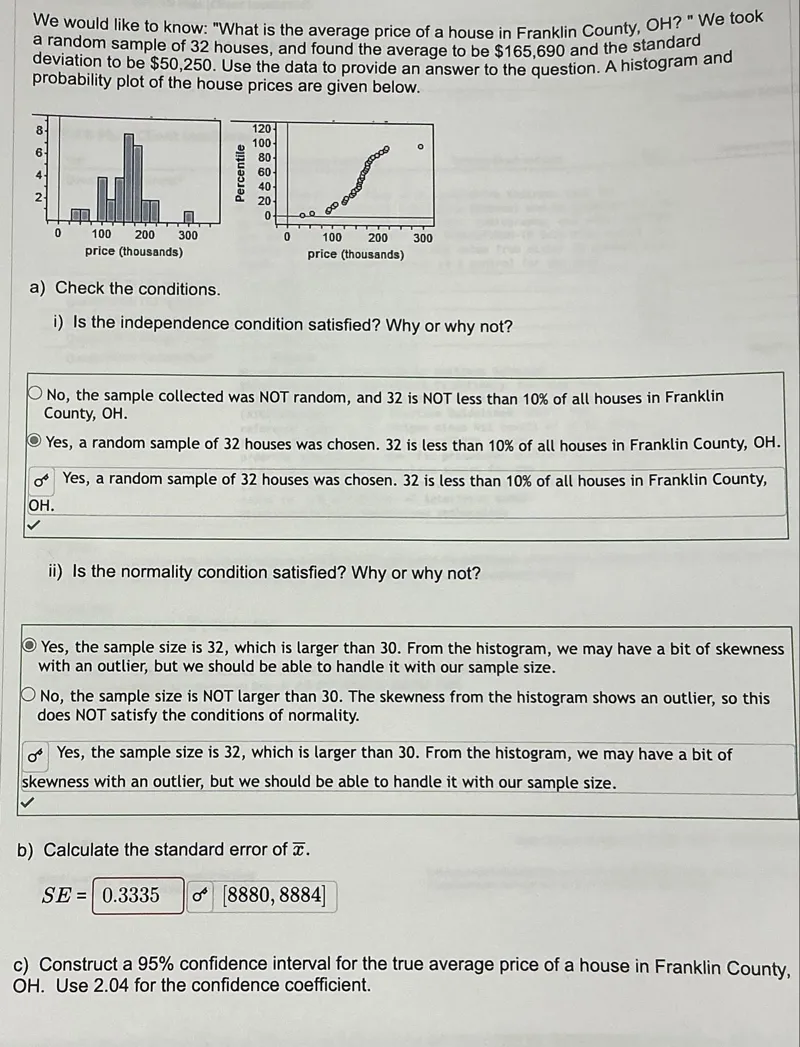
The problem states that "We took a random sample of 32 houses". Random sampling ensures independence. Also, for the 10% condition, the sample size (n=32) must be less than 10% of the population size. It is reasonable to assume that the total number of houses in Franklin County, OH, is much larger than 320 (32 * 10), so 32 houses is less than 10% of all houses in the county.
Therefore, the independence condition is satisfied.
The correct option is: Yes, a random sample of 32 houses was chosen. 32 is less than 10% of all houses in Franklin County, OH.
ii) Is the normality condition satisfied? Why or why not?
The sample size is n=32. According to the Central Limit Theorem (CLT), if the sample size is sufficiently large (typically n ≥ 30), the sampling distribution of the sample mean will be approximately normal, regardless of the shape of the population distribution. Here, n=32, which is greater than 30.
The histogram shows some skewness and possibly an outlier around 300 (thousand dollars). However, with a sample size of 32, the CLT allows us to proceed with methods that assume normality of the sampling distribution of the mean.
Therefore, the normality condition is satisfied due to the large sample size.
The correct option is: Yes, the sample size is 32, which is larger than 30. From the histogram, we may have a bit of skewness with an outlier, but we should be able to handle it with our sample size.
b) Calculate the standard error of $\bar{x}$.
The formula for the standard error of the sample mean ($SE_{\bar{x}}$) is:
$SE_{\bar{x}} = \frac{s}{\sqrt{n}}$
where $s$ is the sample standard deviation and $n$ is the sample size.
Given:
$s = \$50,250$
$n = 32$
$SE_{\bar{x}} = \frac{50,250}{\sqrt{32}}$
$SE_{\bar{x}} = \frac{50,250}{5.65685}$
$SE_{\bar{x}} \approx 8882.00$
The question asks for the standard error in thousands of dollars, as indicated by the input field "0.3335" and "8880, 8884".
If we express $s$ in thousands of dollars, $s = 50.250$ (thousands).
$SE_{\bar{x}} = \frac{50.250}{\sqrt{32}} \approx 8.882$ (thousands).
The provided options for the standard error are 0.3335 and [8880, 8884]. The calculated value 8882.00 falls within the range [8880, 8884].
So, $SE_{\bar{x}} = 8882.00$.
c) Construct a 95% confidence interval for the true average price of a house in Franklin County, OH. Use 2.04 for the confidence coefficient.
The formula for a confidence interval for the mean is:
Confidence Interval = $\bar{x} \pm t^* \times SE_{\bar{x}}$
where $\bar{x}$ is the sample mean, $t^_$ is the critical t-value (confidence coefficient), and $SE_{\bar{x}}$ is the standard error of the mean.
Given:
$\bar{x} = \$165,690$
$t^_ = 2.04$
$SE_{\bar{x}} = \$8882.00$ (from part b)
Lower bound = $\bar{x} - t^* \times SE_{\bar{x}}$
Lower bound = $165,690 - 2.04 \times 8882.00$
Lower bound = $165,690 - 18119.28$
Lower bound = $147,570.72$
Upper bound = $\bar{x} + t^* \times SE_{\bar{x}}$
Upper bound = $165,690 + 2.04 \times 8882.00$
Upper bound = $165,690 + 18119.28$
Upper bound = $183,809.28$
The 95% confidence interval for the true average price of a house in Franklin County, OH, is approximately $(\$147,570.72, \$183,809.28)$.
The final answer for part b) is 8882.00.
The final answer for part c) is (147570.72, 183809.28).
☺
a) i) The independence condition is satisfied because a random sample of 32 houses was chosen, and 32 is less than 10% of all houses in Franklin County, OH.
a) ii) The normality condition is satisfied because the sample size (n=32) is larger than 30, allowing the Central Limit Theorem to apply despite potential skewness or outliers in the population distribution.
b) The standard error of $\bar{x}$ is $8882.00$.
c) The 95% confidence interval for the true average price of a house in Franklin County, OH, is $(\$147,570.72, \$183,809.28)$.