Questions: In the figure, ABCDEFGH is a regular octagon and DEIJK is a regular pentagon. Find x.
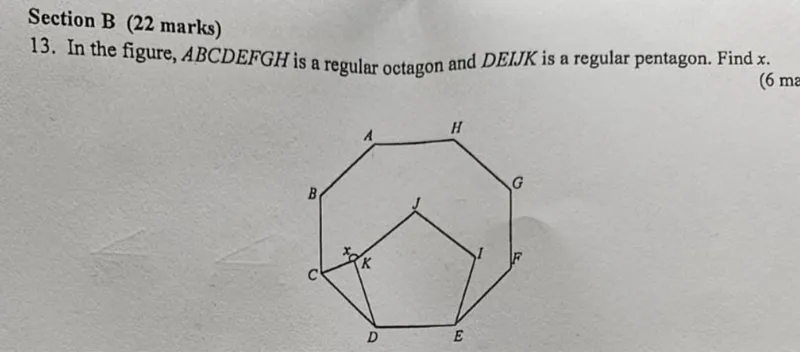
Transcript text: In the figure, $A B C D E F G H$ is a regular octagon and $D E I J K$ is a regular pentagon. Find $x$.





