Questions: Which of the following partial order diagrams is the correct diagram for the divisor order on D24 := 1, 2, 3, 4, 6, 8, 12, 24 ordered by divisibility?
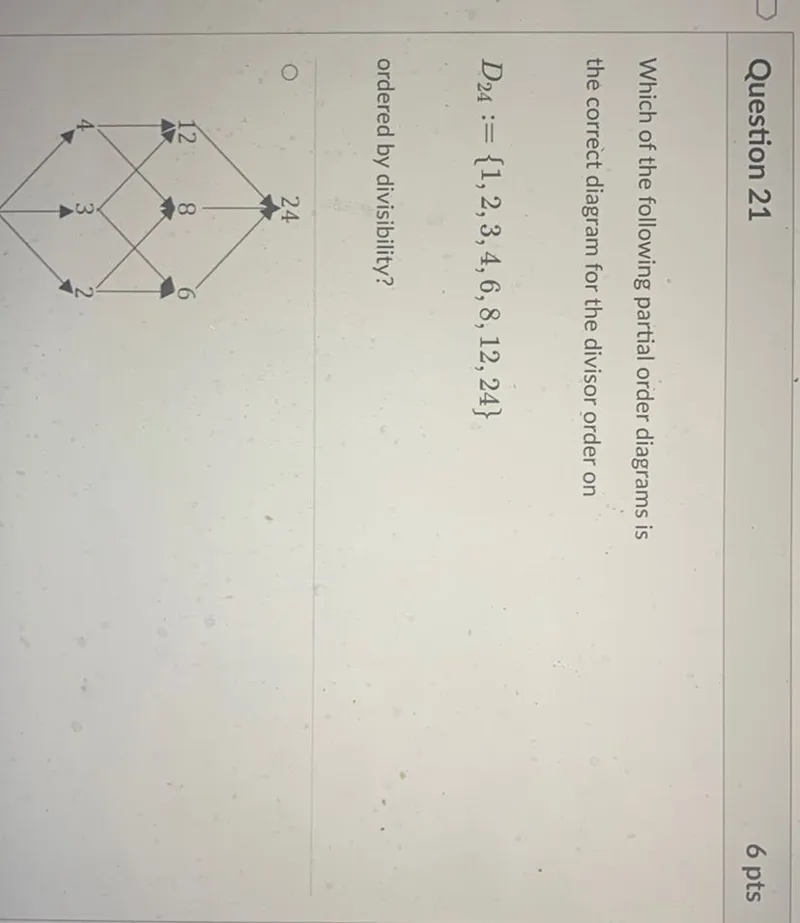
Transcript text: Which of the following partial order diagrams is the correct diagram for the divisor order on \( D_{24}:=\{1,2,3,4,6,8,12,24\} \) ordered by divisibility?





