Questions: Which of the statements a through k about the function y=f(x) graphed here are true, and which are false? a. The statement lim x → 0 f(x) exists is true. b. The statement lim x → 0 f(x)=-2 is □
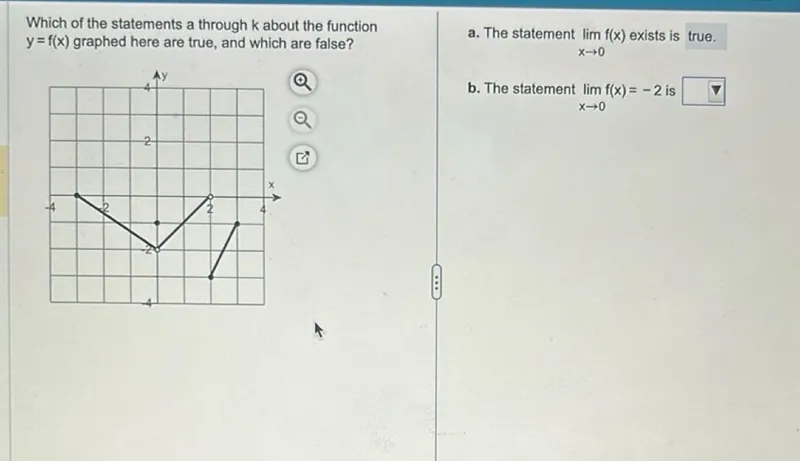
Transcript text: Which of the statements a through $k$ about the function $y=f(x)$ graphed here are true, and which are false?
a. The statement $\lim _{x \rightarrow 0} f(x)$ exists is true.
b. The statement $\lim _{x \rightarrow 0} f(x)=-2$ is $\square$





