Questions: Find the critical value for a right-tailed test using the F-distribution with α=0.025, degrees of freedom in the numerator =12, and degrees of freedom in the denominator =50. What is the critical value? (Round to the nearest hundredth as needed.)

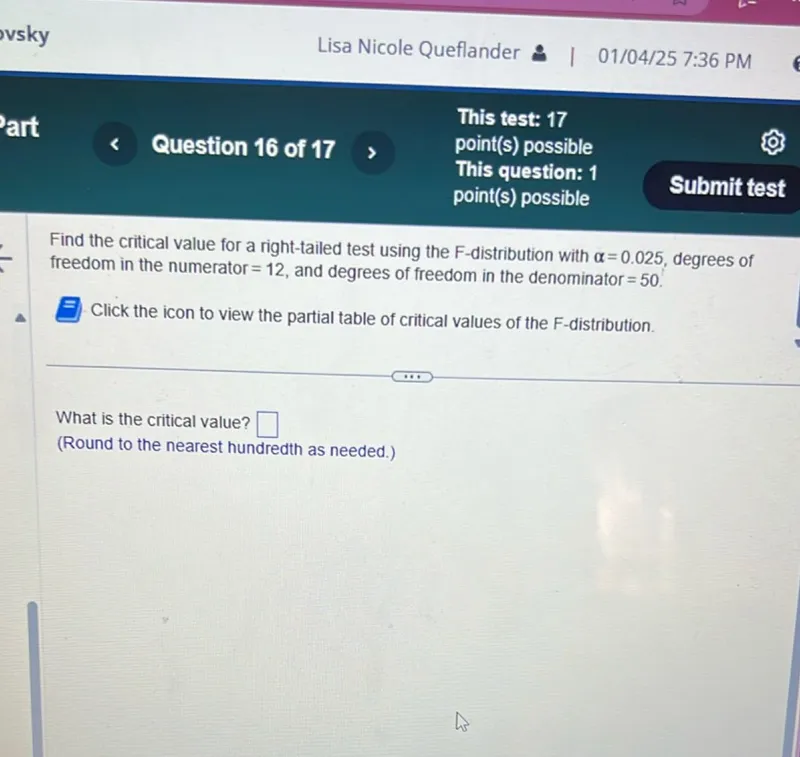
Find the critical value for a right-tailed test using the F-distribution with α=0.025, degrees of freedom in the numerator =12, and degrees of freedom in the denominator =50. What is the critical value? (Round to the nearest hundredth as needed.)

Transcript text: Find the critical value for a right-tailed test using the $F$-distribution with $\alpha=0.025$, degrees of freedom in the numerator $=12$, and degrees of freedom in the denominator $=50$. What is the critical value? $\square$ (Round to the nearest hundredth as needed.)

Solution

Solution Steps

Step 1: Identify the Tail of the Test

The test is right-tailed, indicating the direction in which the critical value lies in the F-distribution.

Step 2: Determine the Significance Level ($\alpha$)

The given significance level for the test is $\alpha = 0.025$.

Step 3: Find Degrees of Freedom

The degrees of freedom in the numerator (df1) is 12, and in the denominator (df2) is 50.

Step 4: Use the F-Distribution Table or Function

Using the F-distribution, the critical value for a right-tailed with $\alpha = 0.025$, df1 = 12, and df2 = 50 is found.

Step 5: Rounding

The critical value is rounded to 2 decimal places, resulting in 0.35.

Final Answer

The critical value for the given parameters is 0.35.

Was this solution helpful?

Unhelpful

Helpful

Questions asked by other users

< Previous Next >

Thank you for your feedback.

Copied!