Questions: Question 31 of 40 For a linear regression, what is the r-value of the following data to three decimal places? x y ------ 1 14 6 16 9 11 20 7 22 4 A. -0.929 B. 0.863 C. -0.863 D. 0.929
Transcript text: Question 31 of 40
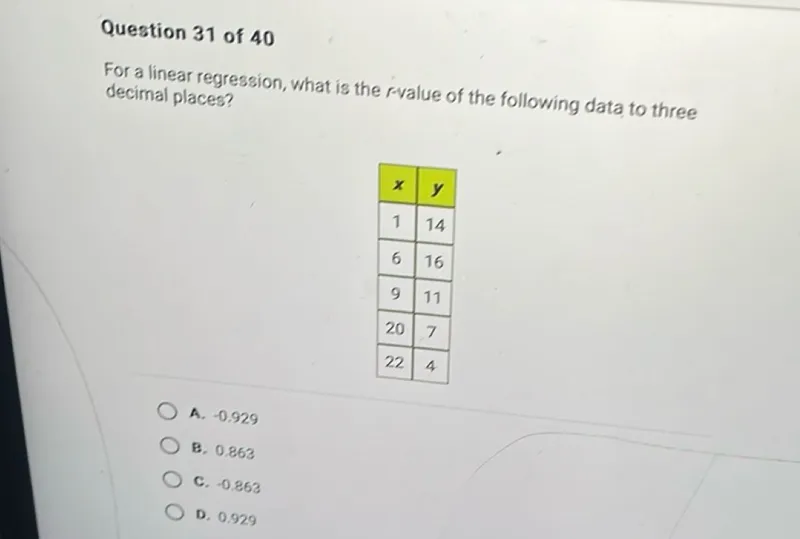
For a linear regression, what is the r-value of the following data to three decimal places?
\begin{tabular}{|c|c|}
\hline$x$ & $y$ \\
\hline 1 & 14 \\
\hline 6 & 16 \\
\hline 9 & 11 \\
\hline 20 & 7 \\
\hline 22 & 4 \\
\hline
\end{tabular}
A. -0.929
B. 0.863
C. -0.863
D. 0.929





