Questions: Graph the following function and then find the specified limit. When necessary, state that the limit does not exist. G(x) is defined as: - x^2, for x<2, - x+2, for x>2. Find the limit of G(x) as x approaches 2. Choose the correct graph below. A. B. C. D. Find the limit of G(x) as x approaches 2. Select the correct choice below and fill in any answer boxes in your choice. A. The limit of G(x) as x approaches 2 is . (Type an integer or a simplified fraction.) B. The limit does not exist.
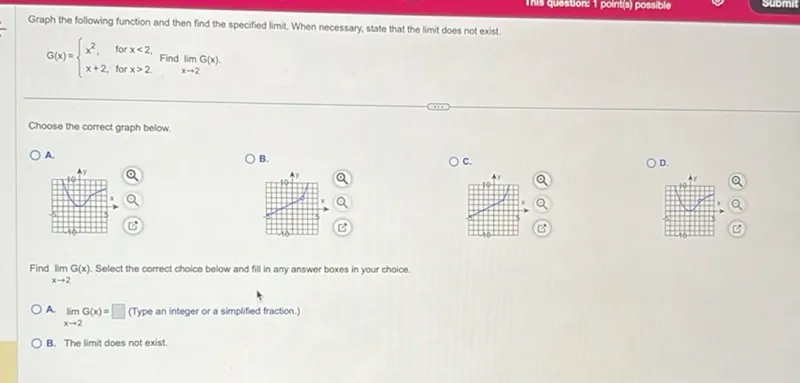
Transcript text: Graph the following function and then find the specified limit. When necessary, state that the limit does not exist.
\[
G(x)=\left\{\begin{array}{ll}
x^{2}, & \text { for } x<2, \\
x+2, & \text { for } x>2
\end{array} \text { Find } \lim _{x \rightarrow 2} G(x)\right.
\]
Choose the correct graph below.
A.
B.
C.
D.
Find $\lim _{x \rightarrow 2} G(x)$. Select the correct choice below and fill in any answer boxes in your choice.
A. $\lim _{x \rightarrow 2} \mathrm{G}(\mathrm{x})=\square$ (Type an integer or a simplified fraction.)
$\square$
B. The limit does not exist.





