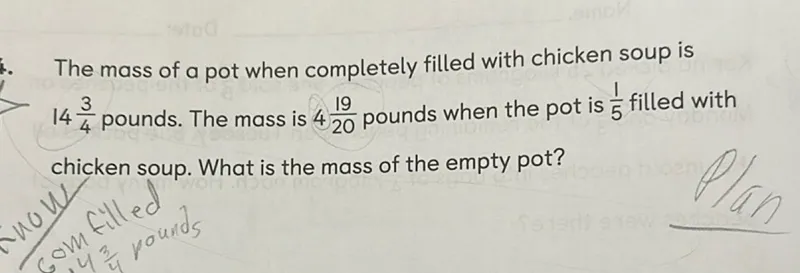Questions: The mass of a pot when completely filled with chicken soup is 14 3/4 pounds. The mass is 4 19/20 pounds when the pot is 1/5 filled with chicken soup. What is the mass of the empty pot?

Solution Steps

Let \( m \) be the mass of the empty pot and \( s \) be the mass of the chicken soup when the pot is completely filled. Based on the problem, we can establish the following equations:

1. \( m + s = 14 \frac{3}{4} \)
2. \( m + \frac{1}{5}s = 4 \frac{19}{20} \)

Convert the mixed numbers to improper fractions for easier calculations:

• \( 14 \frac{3}{4} = \frac{59}{4} \)
• \( 4 \frac{19}{20} = \frac{99}{20} \)

Thus, the equations become:

1. \( m + s = \frac{59}{4} \)
2. \( m + \frac{1}{5}s = \frac{99}{20} \)

We can express the system of equations in matrix form:

\begin{bmatrix} \frac{59}{4} \\ \frac{99}{20} \end{bmatrix} \]

Using Gaussian elimination, we manipulate the augmented matrix:

\[ \left[ A | b \right] = \left[ \begin{array}{cc|c} 1 & 1 & \frac{59}{4} \\ 1 & \frac{1}{5} & \frac{99}{20} \end{array} \right] \]

After performing row operations, we arrive at:

\[ \left[ A | b \right] = \left[ \begin{array}{cc|c} 1 & 0 & \frac{5}{2} \\ 0 & 1 & \frac{49}{4} \end{array} \right] \]

From the final augmented matrix, we can directly read the solutions:

• \( m = \frac{5}{2} \)
• \( s = \frac{49}{4} \)

The mass of the empty pot is \( \frac{5}{2} \) pounds.

Final Answer