Questions: Evaluate the limit. If the limit does not exist, enter DNE. lim (x -> -5) (x^2 - 6x) / (x^2 - x - 30)

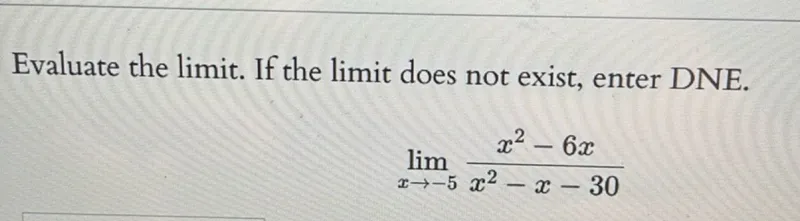
Transcript text: Evaluate the limit. If the limit does not exist, enter DNE. \[ \lim _{x \rightarrow-5} \frac{x^{2}-6 x}{x^{2}-x-30} \]

Solution

Step 1: Substitute the limit value into the expression

Substitute \( x = -5 \) into the expression: \[ \frac{(-5)^{2} - 6(-5)}{(-5)^{2} - (-5) - 30} \]

Step 2: Simplify the numerator and denominator

Calculate the numerator: \[ (-5)^{2} - 6(-5) = 25 + 30 = 55 \] Calculate the denominator: \[ (-5)^{2} - (-5) - 30 = 25 + 5 - 30 = 0 \]

Step 3: Analyze the result

The denominator evaluates to \( 0 \), which means the expression is undefined at \( x = -5 \). Therefore, the limit does not exist (DNE).

\(\boxed{\text{DNE}}\)

Was this solution helpful?

Unhelpful

Helpful

Thank you for your feedback.

Copied!