Questions: Prove that f(x) is continuous at c if and only if the limit as h approaches 0 of f(c+h)=f(c). First, assume f(x) is continuous at c. From the definition of continuity, what is known about the function? - The limit as x approaches c of f(x) exists - The limit as x approaches c of f(x)=f(c) - f(c) exists - All of the above. If the limit as x approaches c of f(x)=f(c), how can this be used to show the limit as h approaches 0 of f(c+h)=f(c)? - Define h equal to x-c. - This cannot be shown. - Define h equal to x+c. - Since h approaches zero, the statements are not equivalent. Now, assume the limit as h approaches 0 of f(c+h)=f(c). Can h be defined so that f(c) and the limit as x approaches c of f(x) exist? - Yes - No
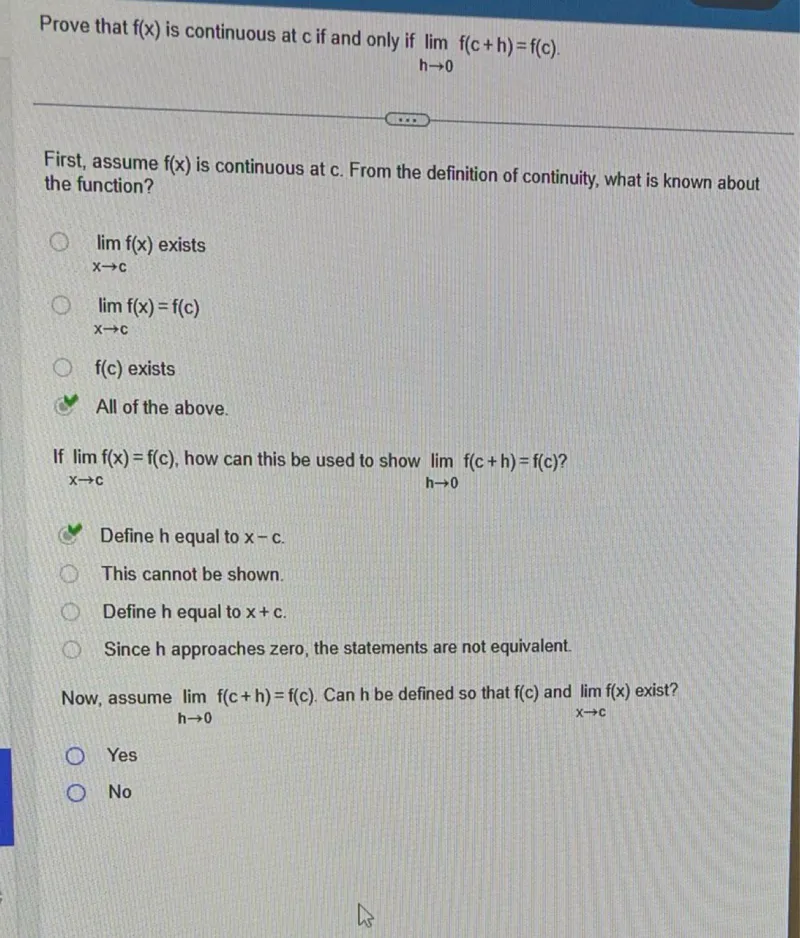
Transcript text: Prove that $f(x)$ is continuous at $c$ if and only if $\lim _{h \rightarrow 0} f(c+h)=f(c)$.
First, assume $f(x)$ is continuous at $c$. From the definition of continuity, what is known about the function?
$\lim _{x \rightarrow c} f(x)$ exists
$\lim _{x \rightarrow c} f(x)=f(c)$
$f(c)$ exists
All of the above.
If $\lim _{x \rightarrow c} f(x)=f(c)$, how can this be used to show $\lim _{h \rightarrow 0} f(c+h)=f(c)$ ?
Define $h$ equal to $x-c$.
This cannot be shown.
Define $h$ equal to $x+c$.
Since $h$ approaches zero, the statements are not equivalent.
Now, assume $\lim _{h \rightarrow 0} f(c+h)=f(c)$. Can $h$ be defined so that $f(c)$ and $\lim _{x \rightarrow c} f(x)$ exist?
Yes
No





