Questions: 1. Consider the surface area of the pyramid shown. (a) Draw a net for the pyramid. Label all sides with measurements. (b) Write an expression for the surface area of the pyramid and then find the surface area.
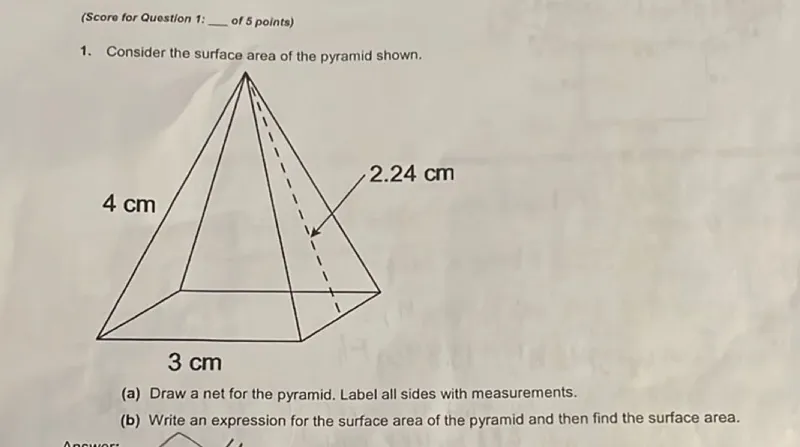
Transcript text: 1. Consider the surface area of the pyramid shown.
(a) Draw a net for the pyramid. Label all sides with measurements.
(b) Write an expression for the surface area of the pyramid and then find the surface area.





