Questions: Imagine you derive the following expression by analyzing the physics of a particular system: a=g sin theta - muk g cos theta, where g=9.80 meter per second squared. Simplify the expression for a by pulling out the common factor. a=(9.80 meter / second squared) sin theta - muk(9.80 meter / second squared) cos theta a=g sin theta - muk g cos theta (no simplification should be performed on the expression in this situation) a=g(sin theta - muk cos theta)

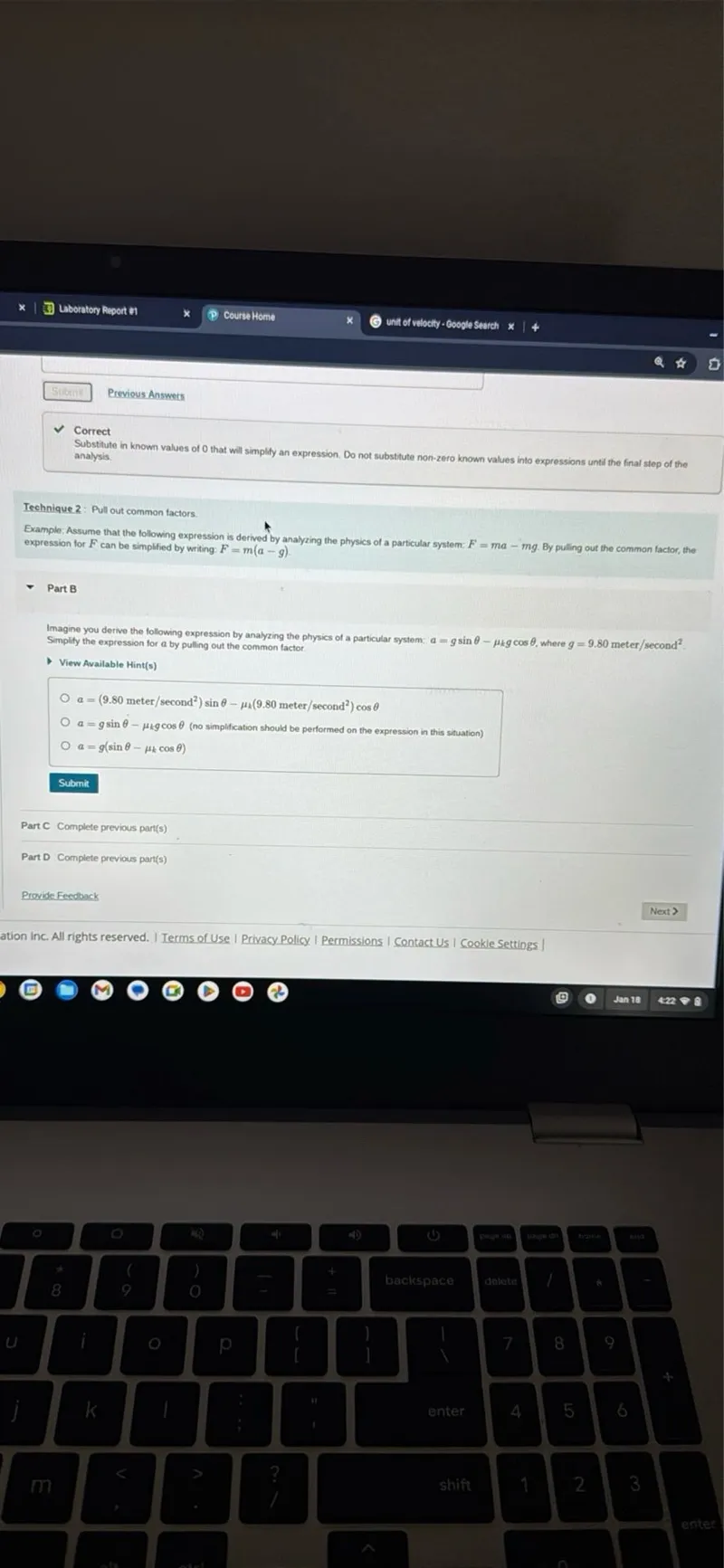
Imagine you derive the following expression by analyzing the physics of a particular system: a=g sin theta - muk g cos theta, where g=9.80 meter per second squared. Simplify the expression for a by pulling out the common factor. a=(9.80 meter / second squared) sin theta - muk(9.80 meter / second squared) cos theta a=g sin theta - muk g cos theta (no simplification should be performed on the expression in this situation) a=g(sin theta - muk cos theta)
Transcript text: Imagine you derive the following expression by analyzing the physics of a particular system: $a=g \sin \theta-\mu_{k} g \cos \theta$, where $g=9.80$ meter $^{\text {Simplity }}$ second ${ }^{2}$. Simplify the expression for $a$ by pulling out the common factor. $a=\left(9.80\right.$ meter $/$ second $\left.{ }^{2}\right) \sin \theta-\mu_{k}\left(9.80\right.$ meter $/$ second $\left.{ }^{2}\right) \cos \theta$ $a=g \sin \theta-\mu_{k} g \cos \theta$ (no simplification should be performed on the expression in this situation) $a=g\left(\sin \theta-\mu_{k} \cos \theta\right)$
failed

Solution

failed
failed

Simplifying the expression for \( a \) by pulling out the common factor.

Identify the common factor

In the expression \( a = g \sin \theta - \mu_{k} g \cos \theta \), the common factor is \( g \).

Factor out the common factor

By factoring out \( g \), the expression becomes \( a = g(\sin \theta - \mu_{k} \cos \theta) \).

\(\boxed{a = g(\sin \theta - \mu_{k} \cos \theta)}\)

The simplified expression for \( a \) by pulling out the common factor is \(\boxed{a = g(\sin \theta - \mu_{k} \cos \theta)}\).

Was this solution helpful?
failed
Unhelpful
failed
Helpful

Questions asked by other users

failedAnswered
Part IV. Essay. 10 Points. Please answer the following as complete as possible. 20. Entropy is a fantastically important concept in thermodynamics and thus it is the focus of one of the laws of thermodynamics (the 2nd one). Tell me why understanding entropy is important in life and death, and chemistry. Use specific examples, equations, and relationships to other chemical concepts. Extra credit (+1): If the ΔG for the reaction C(s, diamond) → C(s, graphite) is -3 kJ, how come are diamonds not spontaneously turning into graphite?
failedAnswered
An archaeon has 9.8 × 10^16 protons and a net charge of 6.6 pC. Part (a) How many fewer electrons are there than protons? Np-Ne=
failedAnswered
The scientific convention of alpha = 0.05 is common practice.
failedAnswered
33. Dusty Rhodes, an Oklahoma resident, died without a written will. Which * 1 point of the following is true? His estate will not go through probate. He has died intestate. His estate will automatically escheat to the county. His will was holographic.
failedAnswered
Question 4 Given the radius r of a sphere, calculate its volume V using the formula V=(4/3) π r^3. Calculate V when r=8 feet and use π=3.14. Round your answer to two decimal places.