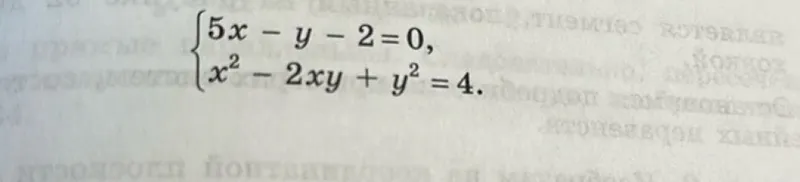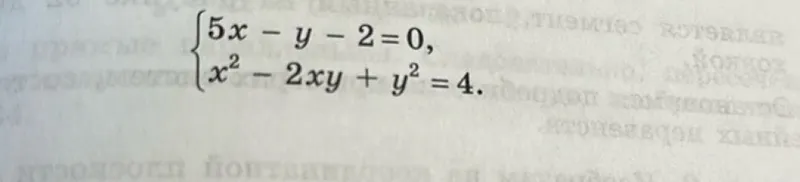Questions: 5x - y - 2 = 0 x^2 - 2xy + y^2 = 4

Solve the system of equations given by \( \left\{\begin{array}{l}5x - y - 2 = 0 \\ x^{2} - 2xy + y^{2} = 4\end{array}\right. \).

Rearranging the first equation for \( y \).

From the equation \( 5x - y - 2 = 0 \), we can express \( y \) as \( y = 5x - 2 \).

Substituting \( y \) into the second equation.

Substituting \( y = 5x - 2 \) into \( x^{2} - 2xy + y^{2} = 4 \) gives us \( x^{2} - 2x(5x - 2) + (5x - 2)^{2} = 4 \).

Solving for \( x \).

The solutions for \( x \) are \( x = 0 \) and \( x = 1 \).

Finding corresponding \( y \) values.

For \( x = 0 \), \( y = 5(0) - 2 = -2 \); for \( x = 1 \), \( y = 5(1) - 2 = 3 \).

The solutions to the system are \( (0, -2) \) and \( (1, 3) \).

The solutions to the system of equations are \( \boxed{(0, -2)} \) and \( \boxed{(1, 3)} \).