Questions: Refer to the graph. How would you describe the value of the slope of this curve? A. The value of the slope is the same between any two points along the curve. B. The value of the slope is greater between points g and h than between points and j. C. The value of the slope is greater between points / and j than between points g and h. D. We cannot determine whether the slope is greater between g and h or / and j because the relationship between "Points on exam" and "Study time" is not linear.
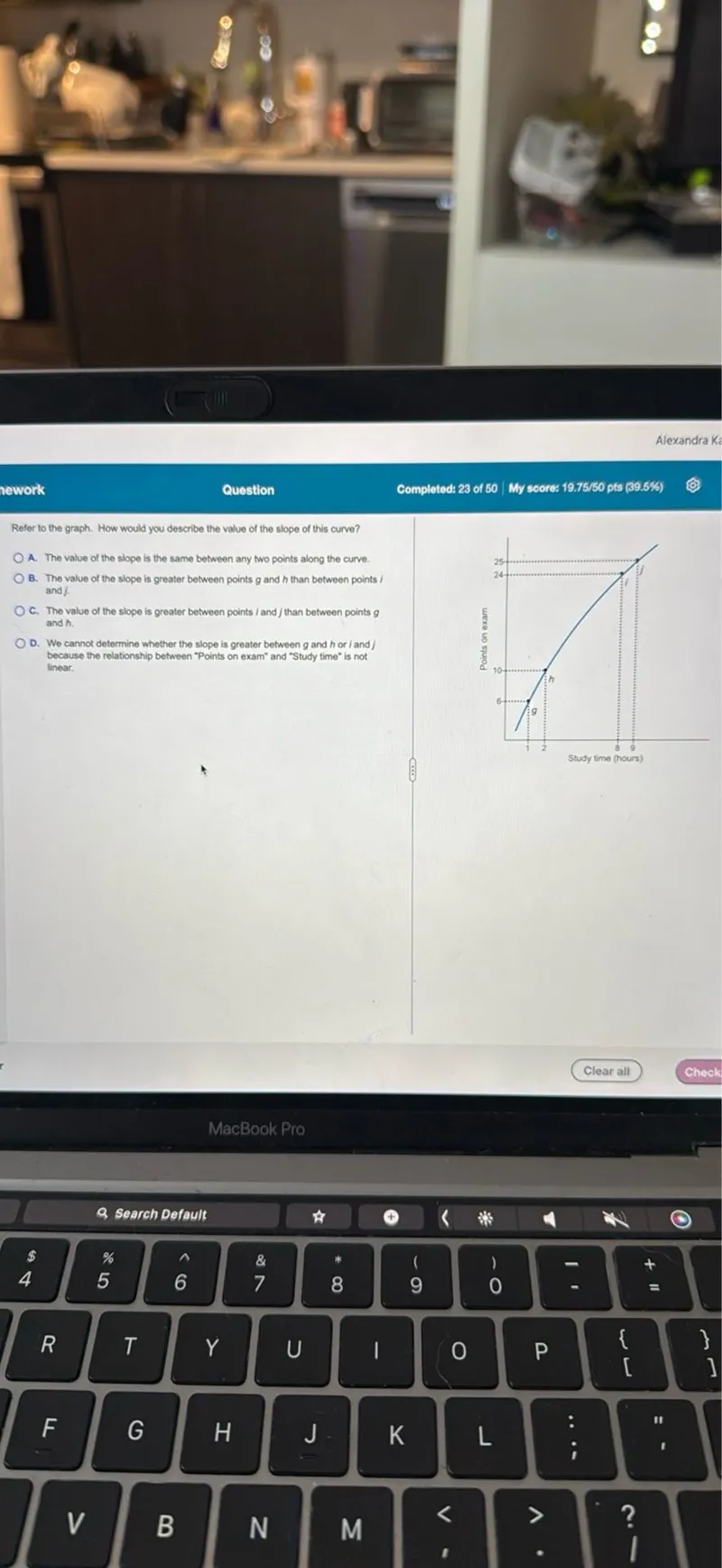
Transcript text: Refer to the graph. How would you describe the value of the slope of this curve?
A. The value of the slope is the same between any two points along the curve.
B. The value of the slope is greater between points $g$ and $h$ than between points and $j$.
C. The value of the slope is greater between points $/$ and $j$ than between points $g$ and $h$.
D. We cannot determine whether the slope is greater between $g$ and $h$ or $/$ and $j$ because the relationship between "Points on exam" and "Study time" is not linear.





