Questions: Write the domain in interval notation. (a) f(x)=(x-2)/(x-81) (b) g(x)=(x-2)/(x^2-81) (c) h(x)=(x-2)/(x^2+81)
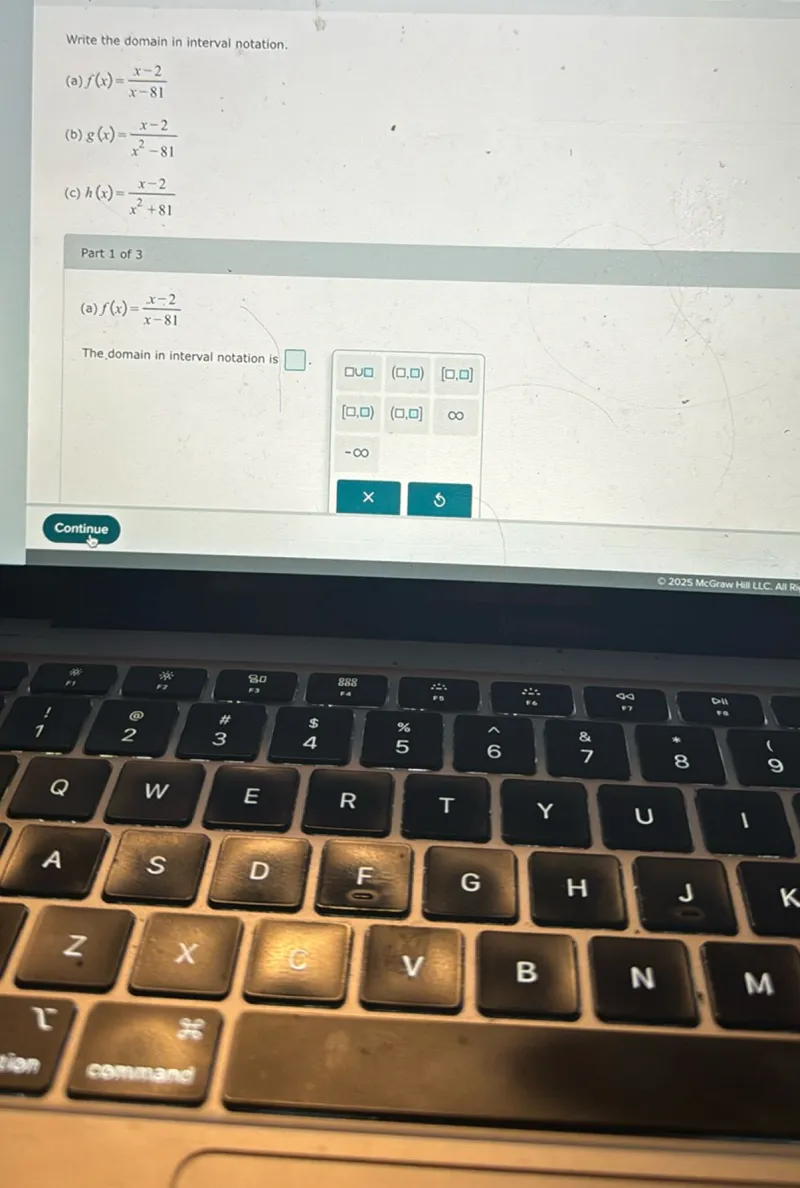
Transcript text: Write the domain in interval notation.
(a) $f(x)=\frac{x-2}{x-81}$
(b) $g(x)=\frac{x-2}{x^{2}-81}$
(c) $h(x)=\frac{x-2}{x^{2}+81}$





