Questions: An example of a(n) number is a square root of a number that is not a perfect square, such as √12. √12=3.46410161513 on and on with NO pattern! rational irrational

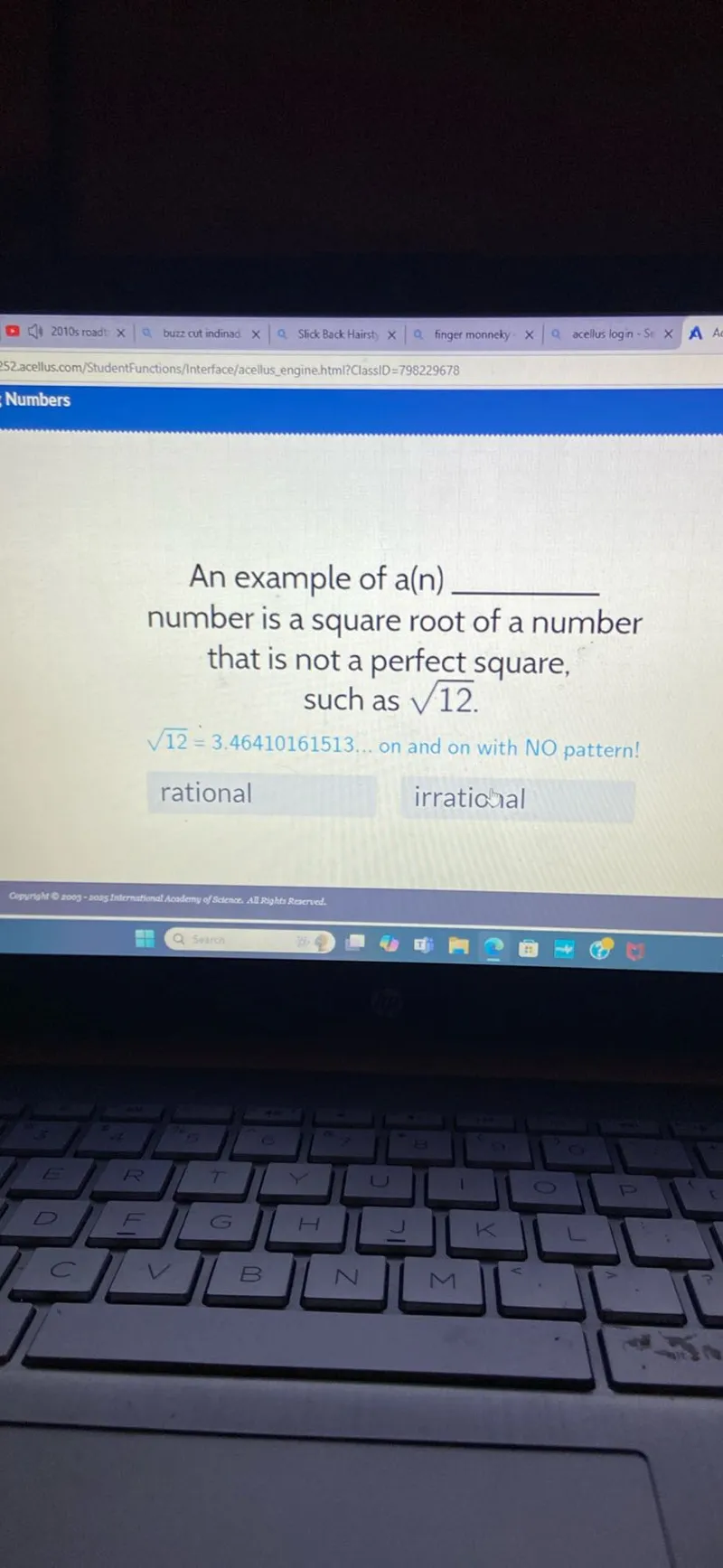
An example of a(n) number is a square root of a number that is not a perfect square, such as √12.
√12=3.46410161513 on and on with NO pattern! rational irrational

Transcript text: An example of a(n) $\qquad$ number is a square root of a number that is not a perfect square, such as $\sqrt{12}$. $\sqrt{12}=3.46410161513 \ldots$ on and on with NO pattern! rational irrational

Solution

Solution Steps

The question seems to be asking about identifying whether a number is rational or irrational. A rational number can be expressed as a fraction of two integers, whereas an irrational number cannot. The square root of a non-perfect square, such as $\sqrt{12}$, is an example of an irrational number because it cannot be expressed as a simple fraction and its decimal representation is non-repeating and non-terminating.

Step 1: Identify the Number

We are given the number $ 12 $ and need to determine whether $ \sqrt{12} $ is rational or irrational.

Step 2: Calculate the Square Root

The square root of $ 12 $ can be expressed as: \[ \sqrt{12} = \sqrt{4 \times 3} = 2\sqrt{3} \] Since $ \sqrt{3} $ is not a perfect square, $ \sqrt{12} $ cannot be expressed as a fraction of two integers.

Step 3: Determine Rationality

A number is considered irrational if it cannot be expressed as $ \frac{a}{b} $ where $ a $ and $ b $ are integers and $ b \neq 0 $. Since $ \sqrt{12} $ has a non-repeating and non-terminating decimal expansion, it is classified as an irrational number.