Questions: The equation (y=4 cdot 3^t) shows the number of infected people from an outbreak of the measles. The variable (y) represents the number of infected people, and (t) represents time in weeks. In how many weeks will the number of infected people reach 600?
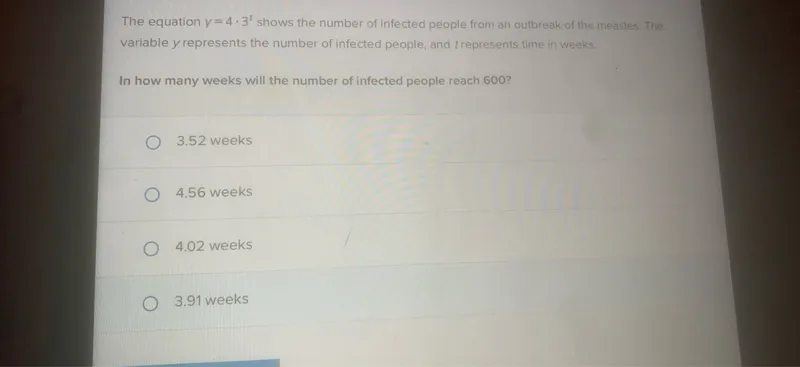
Transcript text: The equation $y=4 \cdot 3^{t}$ shows the number of infected people from an outbreak of the measles. The variable $y$ represents the number of infected people, and $t$ represents time in weeks.
In how many weeks will the number of infected people reach 600 ?
3.52 weeks
4.56 weeks
4.02 weeks
3.91 weeks





