Questions: A sample of 75 heads of lettuce was selected. Assume that the population distribution of head weight is normal. The weight of each head of lettuce was then recorded. The mean weight was 2.3 pounds with a standard deviation of 0.21 pounds. The population standard deviation is known to be 0.24 pounds. Find the 98% confidence interval. Round all answers to the nearest hundredth. a. Find x̄. x̄=2.3 b. Find s and σ. Enter DNE if they are unknown. s=0.21 σ=0.24 c. Find n. n=75 d. Identify the type of confidence interval. Select an answer - e. Find the Critical Value. ? = f. Find the 98% confidence interval and complete the sentence below. Conclusion: We estimate with % confidence that the population mean time needed is between and hours.

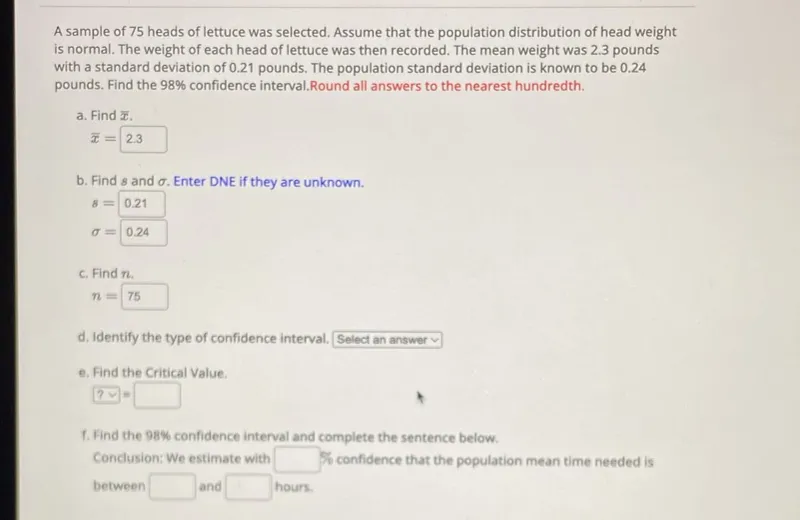
A sample of 75 heads of lettuce was selected. Assume that the population distribution of head weight is normal. The weight of each head of lettuce was then recorded. The mean weight was 2.3 pounds with a standard deviation of 0.21 pounds. The population standard deviation is known to be 0.24 pounds. Find the 98% confidence interval. Round all answers to the nearest hundredth.

a. Find x̄.
x̄=2.3

b. Find s and σ. Enter DNE if they are unknown.
s=0.21
σ=0.24

c. Find n.
n=75

d. Identify the type of confidence interval. Select an answer -

e. Find the Critical Value.
? =

f. Find the 98% confidence interval and complete the sentence below.

Conclusion: We estimate with % confidence that the population mean time needed is between and hours.

Transcript text: A sample of 75 heads of lettuce was selected. Assume that the population distribution of head weight is normal. The weight of each head of lettuce was then recorded. The mean weight was 2.3 pounds with a standard deviation of 0.21 pounds. The population standard deviation is known to be 0.24 pounds. Find the $98 \%$ confidence interval.Round all answers to the nearest hundredth. a. Find $\bar{x}$. \[ \bar{x}=2.3 \] b. Find $s$ and $\sigma$. Enter DNE if they are unknown. \[ \begin{array}{l} s=0.21 \\ \sigma=0.24 \end{array} \] c. Find $n$. \[ n=75 \] d. Identify the type of confidence interval. Select an answer - e. Find the Critical Value. \[ \text { ? }= \] f. Find the $98 \%$ confidence interval and complete the sentence below. Conclusion: We estimate with $\square$ \% confidence that the population mean time needed is between $\square$ and $\square$ hours.

Solution

Solution Steps

Step 1: Calculate the Sample Mean

The sample mean weight of the heads of lettuce is given by: \[ \bar{x} = 2.3 \]

Step 2: Identify the Sample and Population Standard Deviations

The sample standard deviation $ s $ and the population standard deviation $ \sigma $ are: \[ s = 0.21 \] \[ \sigma = 0.24 \]

Step 3: Determine the Sample Size

The sample size $ n $ is: \[ n = 75 \]

Step 4: Identify the Type of Confidence Interval

Since the population standard deviation is known, we will use the Z-distribution to calculate the confidence interval.

Step 5: Find the Critical Value

The critical value $ z $ for a $ 98\% $ confidence level is calculated as: \[ z = 0.99 \]

Step 6: Calculate the Confidence Interval

The confidence interval for the mean is given by the formula: \[ \bar{x} \pm z \frac{\sigma}{\sqrt{n}} \] Substituting the values: \[ 2.3 \pm 0.99 \cdot \frac{0.24}{\sqrt{75}} \approx 2.3 \pm 0.06 \] This results in the confidence interval: \[ (2.24, 2.36) \]

Step 7: Conclusion

We estimate with $ 98.0\% $ confidence that the population mean weight is between $ 2.24 $ and $ 2.36 $ pounds.