Questions: Kevin examines the following data, which shows the balance in an investment account. - Year 1: 2,000.00 - Year 2: 2,120.00 - Year 3: 2,247.20 - Year 5: 2,382.03 What is the formula for the geometric sequence represented by the data above? - (an=2000(1.6)^n-1) - (an=2000(1.06)^n-1) - (an=2000(1.6)^n)
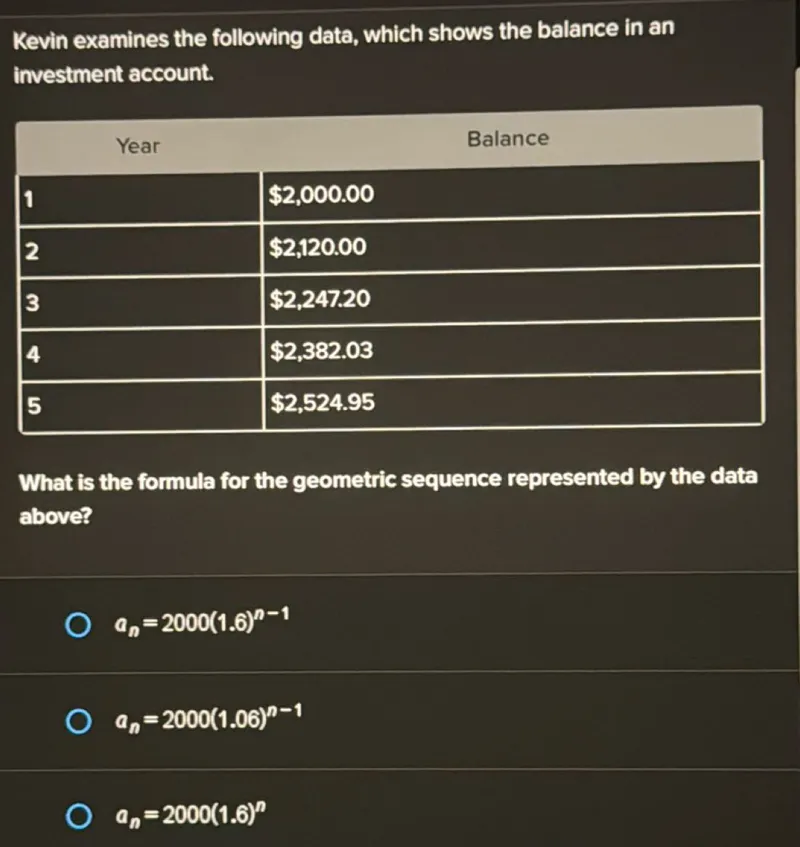
Transcript text: Kevin examines the following data, which shows the balance in an investment account.
\begin{tabular}{|l|l|}
\hline \multicolumn{2}{|c|}{ Year } \\
\hline $\mathbf{1}$ & $\$ 2,000.00$ \\
\hline 2 & $\$ 2,120.00$ \\
\hline $\mathbf{3}$ & $\$ 2,247.20$ \\
\hline $\mathbf{5}$ & $\$ 2,382.03$ \\
\hline
\end{tabular}
What is the formula for the geometric sequence represented by the data above?
$a_{n}=2000(1.6)^{n-1}$
$a_{n}=2000(1.06)^{n-1}$
$a_{n}=2000(1.6)^{n}$





