Questions: Multiply as indicated. (15y+39)/(y^2+4y) * (y+4)/(5y+13) (15y+39)/(y^2+4y) * (y+4)/(5y+13) = □ (Simplify your answer.)

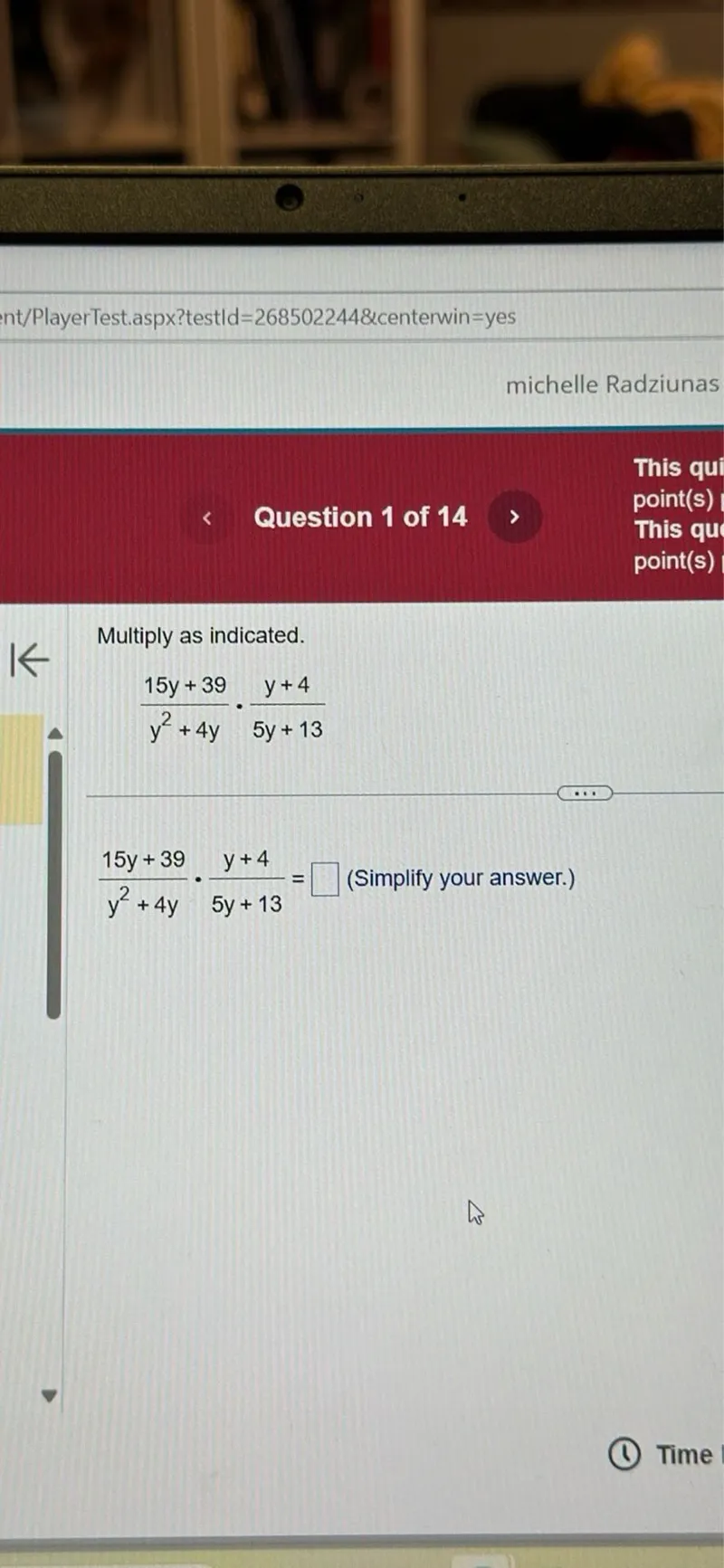
Transcript text: Multiply as indicated. \[ \frac{15 y+39}{y^{2}+4 y} \cdot \frac{y+4}{5 y+13} \] $\frac{15 y+39}{y^{2}+4 y} \cdot \frac{y+4}{5 y+13}=\square$ (Simplify your answer.)

Solution

Solution Steps

Step 1: Factor the Numerator and Denominator

We start with the expression: \[ \frac{15 y + 39}{y^{2} + 4 y} \cdot \frac{y + 4}{5 y + 13} \] First, we factor the numerator $15 y + 39$ and the denominator $y^{2} + 4 y$:

The numerator can be factored as: \[ 15 y + 39 = 3(5 y + 13) \]
The denominator can be factored as: \[ y^{2} + 4 y = y(y + 4) \]

Step 2: Rewrite the Expression

Substituting the factored forms back into the expression, we have: \[ \frac{3(5 y + 13)}{y(y + 4)} \cdot \frac{y + 4}{5 y + 13} \]

Step 3: Cancel Common Factors

Next, we can cancel the common factors in the numerator and denominator:

The factor $5 y + 13$ in the numerator of the first fraction and the denominator of the second fraction cancels out.
The factor $y + 4$ in the numerator of the second fraction and the denominator of the first fraction also cancels out.

After canceling, we are left with: \[ \frac{3}{y} \]

Step 4: Final Simplified Expression

The final simplified expression is: \[ \frac{3}{y} \]