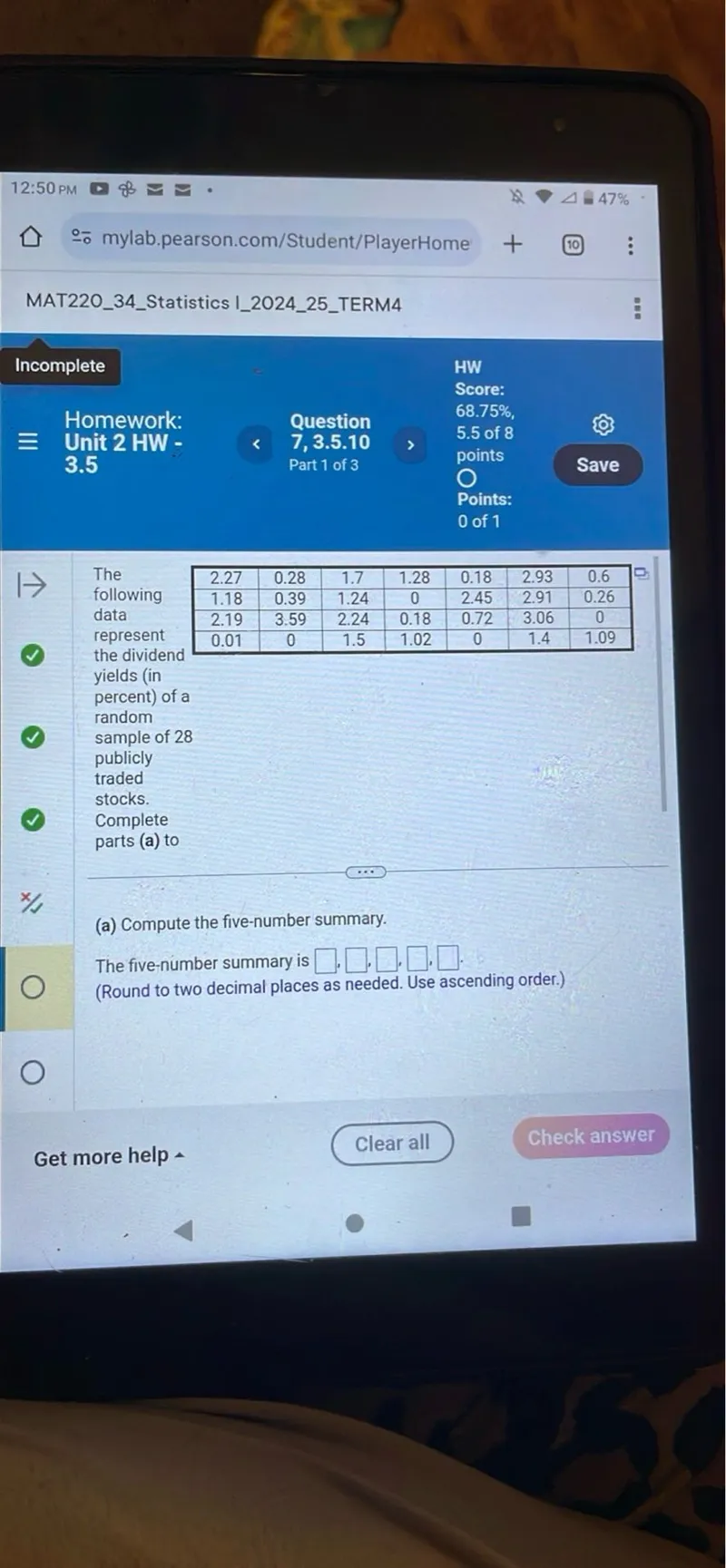
Questions: Homework: 3.5 HW Score: 68.75%, 5.5 of 8 points Points: 0 of 1 Part 1 of 3 2.27 0.28 1.7 1.28 0.18 2.93 0.6 1.18 0.39 1.24 0 2.45 2.91 0.26 2.19 3.59 2.24 0.18 0.72 3.06 0 0.01 0 1.5 1.02 0 1.4 1.09 the dividend yields (in percent) of a random sample of 28 publicly traded stocks. Complete parts (a) to (a) Compute the five-number summary. The five-number summary is . , . (Round to two decimal places as needed. Use ascending order.)

Solution Steps

The first step is to sort the given data in ascending order. The sorted data is: \[ [0, 0, 0, 0, 0.01, 0.18, 0.18, 0.26, 0.28, 0.39, 0.6, 0.72, 1.02, 1.09, 1.18, 1.24, 1.28, 1.4, 1.5, 1.7, 2.19, 2.24, 2.27, 2.45, 2.91, 2.93, 3.06, 3.59] \]

The minimum value of the dataset is: \[ \text{Minimum} = 0 \]

To find the first quartile \( Q_1 \), we use the formula for the rank: \[ \text{Rank} = Q \times (N + 1) = 0.25 \times (28 + 1) = 7.25 \] Since the rank is not an integer, we average the values at ranks 7 and 8: \[ Q_1 = \frac{X_{\text{lower}} + X_{\text{upper}}}{2} = \frac{0.18 + 0.26}{2} = 0.22 \]

To find the median \( Q_2 \), we calculate the rank: \[ \text{Rank} = Q \times (N + 1) = 0.5 \times (28 + 1) = 14.5 \] Again, since the rank is not an integer, we average the values at ranks 14 and 15: \[ Q_2 = \frac{X_{\text{lower}} + X_{\text{upper}}}{2} = \frac{1.09 + 1.18}{2} = 1.14 \]

To find the third quartile \( Q_3 \), we calculate the rank: \[ \text{Rank} = Q \times (N + 1) = 0.75 \times (28 + 1) = 21.75 \] Since the rank is not an integer, we average the values at ranks 21 and 22: \[ Q_3 = \frac{X_{\text{lower}} + X_{\text{upper}}}{2} = \frac{2.19 + 2.24}{2} = 2.21 \]

The maximum value of the dataset is: \[ \text{Maximum} = 3.59 \]

The five-number summary is: \[ \text{Five-number summary} = (0, 0.22, 1.14, 2.21, 3.59) \]

Final Answer