Questions: Here is a data set summarized as a stem-and-leaf plot: 4 023356999 5 02223333457788 6 04555 7 458 How many data values are in this data set? n=31 What is the minimum value in the last class? ans =74 What is the frequency of the modal class? (Hint, what is the mode?) frequency = How many of the original values are greater than 50 ? ans = 21
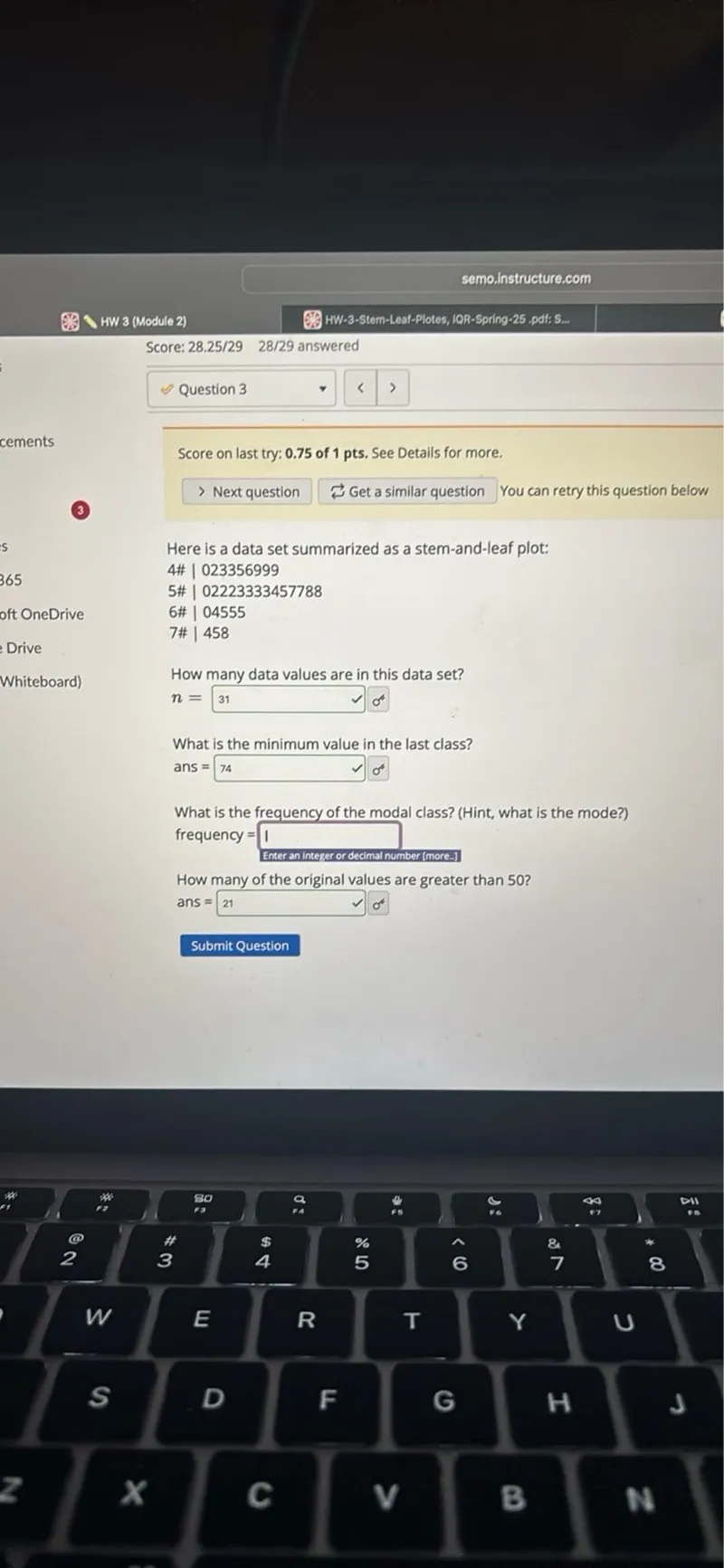
Transcript text: Here is a data set summarized as a stem-and-leaf plot:
4\# | 023356999
5\# | 02223333457788
6\# | 04555
7\# | 458
How many data values are in this data set?
\[
n=31 \quad
\]
What is the minimum value in the last class?
\[
\text { ans }=74
\]
What is the frequency of the modal class? (Hint, what is the mode?)
frequency = $\square$
How many of the original values are greater than 50 ?
ans $=$ $\square$
21





