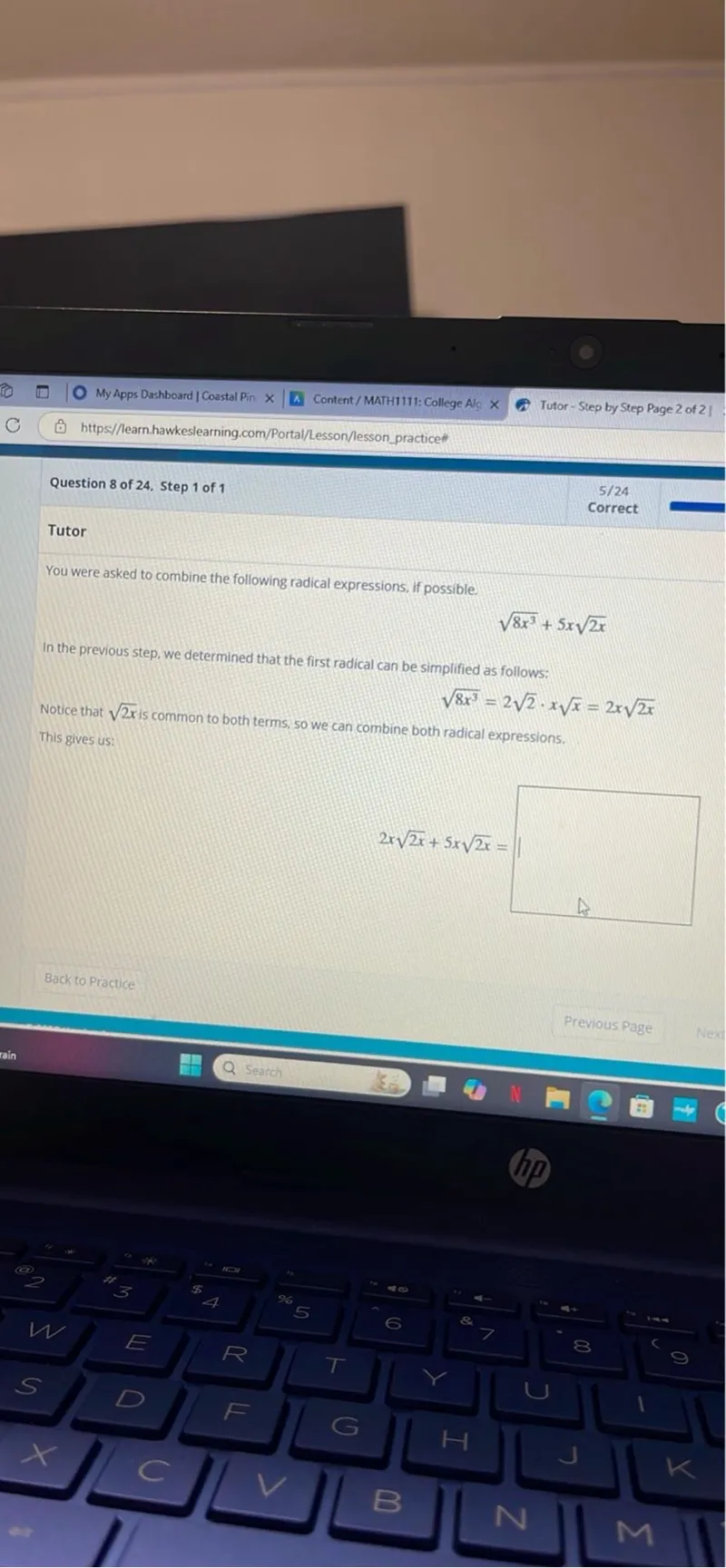
Questions: You were asked to combine the following radical expressions, if possible. sqrt(8 x^3) + 5 x sqrt(2 x) In the previous step, we determined that the first radical can be simplified as follows: sqrt(8 x^3) = 2 sqrt(2) * x sqrt(x) = 2 x sqrt(2 x) Notice that sqrt(2 x) is common to both terms, so we can combine both radical expressions. This gives us: 2 x sqrt(2 x) + 5 x sqrt(2 x) =

Transcript text: My Apps Dashboard | Coastal Pin Content / MATH1111: College Alg $\times$ Tutor - Step by Step Page 2 of 21 https//learn.hawkeslearning.com/Portal/Lesson/lesson_practice\# Question 8 of 24, Step 1 of 1 5/24 Correct Tutor You were asked to combine the following radical expressions, if possible. \[ \sqrt{8 x^{3}}+5 x \sqrt{2 x} \] In the previous step, we determined that the first radical can be simplified as follows: \[ \sqrt{8 x^{3}}=2 \sqrt{2} \cdot x \sqrt{x}=2 x \sqrt{2 x} \] Notice that $\sqrt{2 x}$ is common to both terms, so we can combine both radical expressions. This gives us: $\square$ \[ 2 x \sqrt{2 x}+5 x \sqrt{2 x}= \] Back to Practice Previous Page