Questions: Factor out the greatest common factor. If the greatest common factor is 1, just retype the polynomial. 24 h^3 - 36 h^2
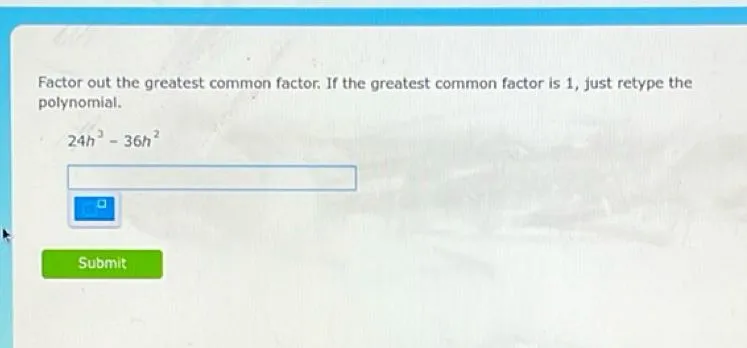
Transcript text: Factor out the greatest common factor. If the greatest common factor is 1 , just retype the polynomial.
\[
24 h^{3}-36 h^{2}
\]
$\square$
Submit





