Questions: Determine whether the equation defines y as a function of x. 2x-3y=5 The equation defines y as a function of x. The equation does not define y as a function of x. Determine whether the equation defines y as a function of x. x^2+(y-5)^2=6 The equation defines y as a function of x. The equation does not define y as a function of x.

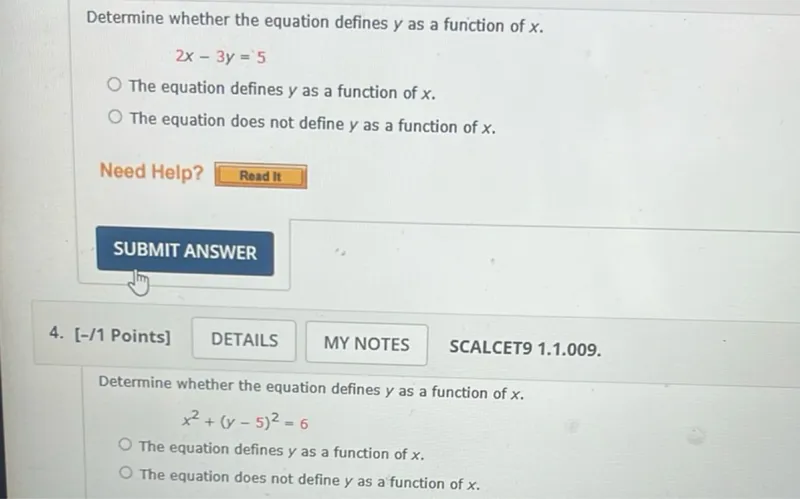
Determine whether the equation defines y as a function of x. 2x-3y=5 The equation defines y as a function of x. The equation does not define y as a function of x. Determine whether the equation defines y as a function of x. x^2+(y-5)^2=6 The equation defines y as a function of x. The equation does not define y as a function of x.
Transcript text: Determine whether the equation defines $y$ as a function of $x$. \[ 2 x-3 y=5 \] The equation defines $y$ as a function of $x$. The equation does not define $y$ as a function of $x$. Determine whether the equation defines $y$ as a function of $x$. \[ x^{2}+(y-5)^{2}=6 \] The equation defines $y$ as a function of $x$. The equation does not define $y$ as a function of $x$.
failed

Solution

failed
failed

Solution Steps

Step 1: Solve for \( y \) in the first equation

Start with the equation: \[ 2x - 3y = 5 \] Subtract \( 2x \) from both sides: \[ -3y = -2x + 5 \] Divide both sides by \( -3 \): \[ y = \frac{2x - 5}{3} \] Since \( y \) is expressed explicitly as a function of \( x \), the equation defines \( y \) as a function of \( x \).

Step 2: Analyze the second equation for \( y \) as a function of \( x \)

Consider the equation: \[ x^{2} + (y-5)^{2} = 6 \] This is the equation of a circle with center \( (0, 5) \) and radius \( \sqrt{6} \). For a given \( x \), there are two possible values of \( y \) (one above and one below the center). Therefore, \( y \) is not uniquely determined by \( x \), and the equation does not define \( y \) as a function of \( x \).

Step 3: Conclusion for the first equation

The first equation \( 2x - 3y = 5 \) defines \( y \) as a function of \( x \) because \( y \) can be expressed explicitly as \( y = \frac{2x - 5}{3} \).

Step 4: Conclusion for the second equation

The second equation \( x^{2} + (y-5)^{2} = 6 \) does not define \( y \) as a function of \( x \) because \( y \) is not uniquely determined for a given \( x \).

Final Answer

For the first equation: \( \boxed{\text{The equation defines } y \text{ as a function of } x.} \)
For the second equation: \( \boxed{\text{The equation does not define } y \text{ as a function of } x.} \)

Was this solution helpful?
failed
Unhelpful
failed
Helpful

Questions asked by other users

failedAnswered
Q1.11. Now examine the lower panel (butterflies), where the curve continues to rise linearly. What does this indicate about the processes structuring the butterfly community? It suggests that the communities are unsaturated and that the size of the regional pool determines local species richness. It suggests that the communities are becoming saturated and that local processes are likely becoming increasingly important. It does not tell us anything about the relative importance of the regional species pool and local interactions.
failedAnswered
Which type of medication treats a sprained ankle that exhibits pain, redness, and heat? antihistamine anti-inflammatory antibiotic antiparasitic
failedAnswered
Let two cards be dealt successively, without replacement, from a standard 52-card deck. Find the probability of the event. two queens The probability of drawing two queens is (Simplify your answer. Type an integer or a fraction.)
failedAnswered
Calculate the sample standard deviation and sample variance for the following frequency distribution of heart rates for a sample of American adults. If necessary, round to one more decimal place than the largest number of decimal places given in the data. Heart Rates in Beats per Minute Class Frequency 56-62 10 63-69 5 70-76 5 77-83 8 84-90 13
failedAnswered
D1. During a midterm exam, you toss your pencil straight up in the air and catch it 2.00 s later at the same height as the point of release. (a) What is the acceleration (magnitude and direction) of the pencil at maximum height? (1 mark) pencil is in free-fall a=g downward (b) What is the speed of the pencil at maximum height? (1 mark) Since the pencil is thrown straight up, v=0 at maximum height. (c) Calculate the initial speed of the pencil. (2 marks) ttot=2.00 s ; Δy=0 (returns to initial height) Δy=v0y t+1/2 ay t^2 0=v0y t+1/2 ay t^2 => 0=v0y+1/2 ay t => v0y=-1/2 ay t v0y=-1/2(-g) t v0y=1/2 g t (d) Calculate the maximum height that the pencil reaches. If you did not obtain an answer for (c), use a value of 9.50 m/s. ( 3 marks) vy^2=v0y^2+2 ay Δy vy=0 at max. height 4.90 m Therefore 0=v0y^2+2 ay Δymax => Δymax=-v0y^2/2 ay=-(v0y^2)/2(-g) Δymax=-(9.80 m/s)^2/(2(-9.80 m/s^2))=4.90 m (e) If the pencil was only tossed half as high, how long would it be in the air? If you did not obtain an answer for (d), use a value of 5.00 m . ( 3 marks) Δymax=1/2(4.90 m)=2.45 m vy^2=v0y^2+2 ay Δy 0=v0y^2+2 ay Δymax => v0y=sqrt(-2 ay Δymax)=sqrt(-2(-g)(Δymax)) v0y=sqrt(2 g Δymax)=sqrt(2(9.80 m/s^2)(2.45 m))=6.93 m/s From symmetry of motion, for whole flight vy=-v0y Therefore vy=v0y+ay t => -v0y=v0y-g t t=-2 v0y/g=2(6.93 m/s)/(9.80 m/s^2)= Δytot=v0y tb+t+1/2 ay ttot^2 0=vby ttot+1/2(-g) ttot^2 ttot=-v0y(2)/-g=1.415