Questions: Find m angle E. Write your answer as an integer or as a decimal rounded to the nearest tenth. m angle E =
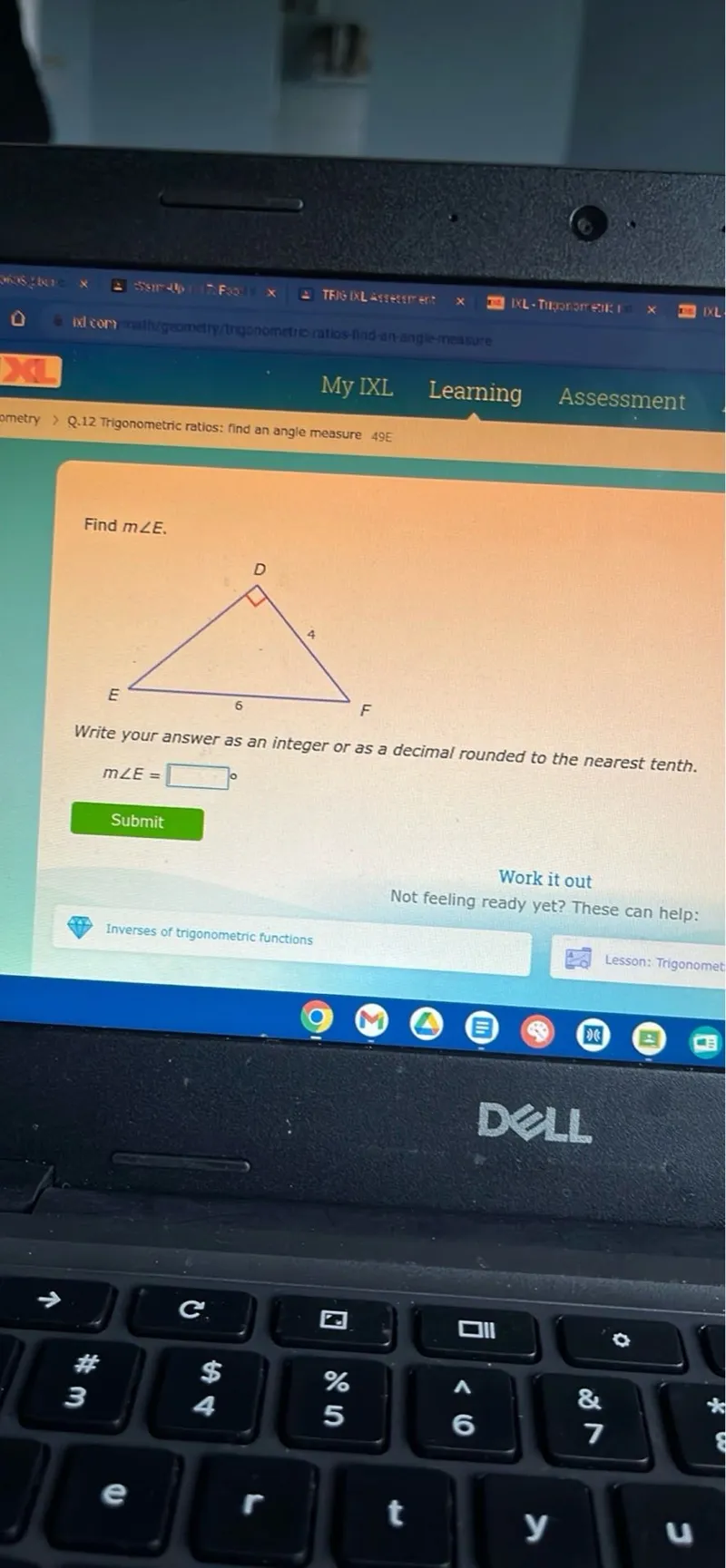
Transcript text: Find $m \angle E$.
Write your answer as an integer or as a decimal rounded to the nearest tenth.
\[
m \angle E=\square
\]





