Questions: Find the following limit. lim x→-5 (-x^2 + 2x - 3) Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. lim x→-5 (-x^2 + 2x -3) = □ (Simplify your answer.) □ B. The limit does not exist.

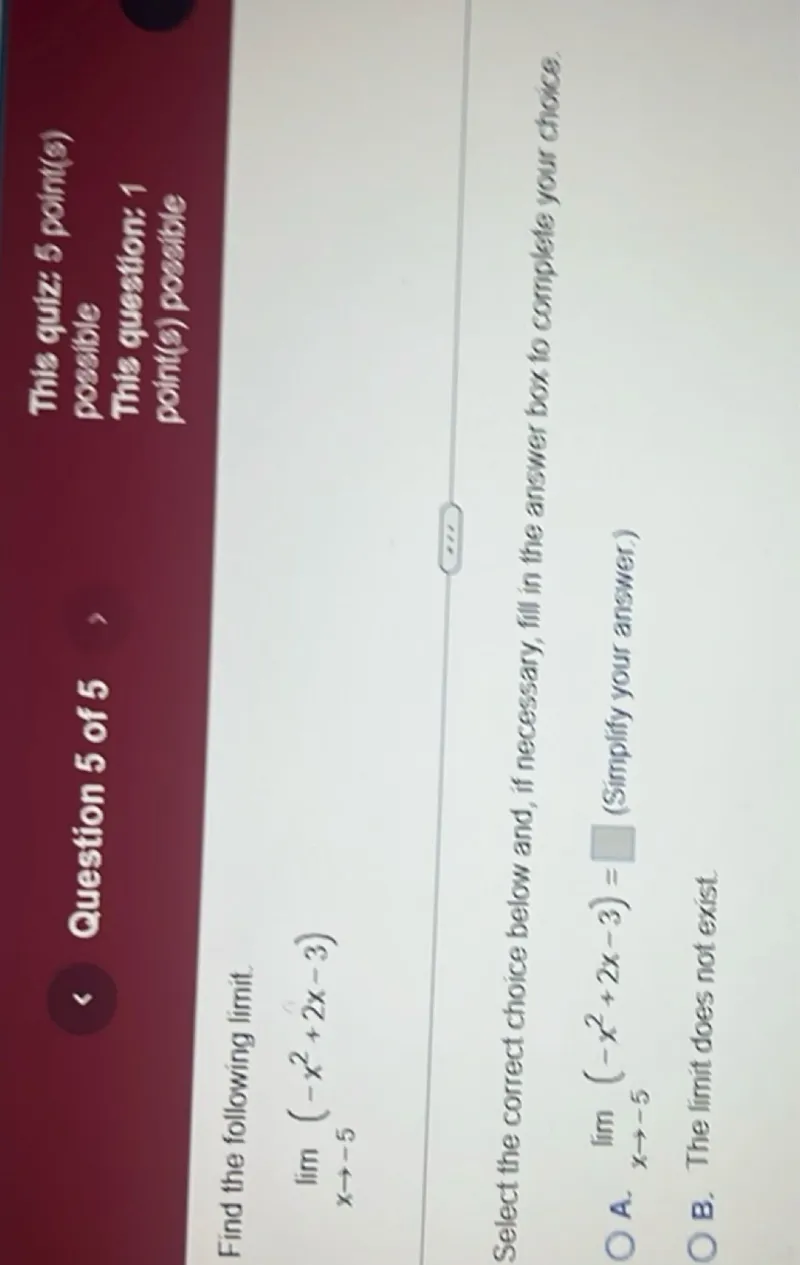
Find the following limit.
lim x→-5 (-x^2 + 2x - 3)

Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. lim x→-5 (-x^2 + 2x -3) = □ (Simplify your answer.)
□
B. The limit does not exist.

Transcript text: Find the following limit. \[ \lim _{x \rightarrow-5}\left(-x^{2}+2 x-3\right) \] Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. $\lim _{x \rightarrow-5}\left(-x^{2}+2 x-3\right)=\square$ (Simplify your answer.) $\square$ B. The limit does not exist.

Solution

Solution Steps

Step 1: Substitute the value of $ x $ into the function

To find the limit as $ x $ approaches $-5$, substitute $ x = -5 $ directly into the function: \[ \lim _{x \rightarrow-5}\left(-x^{2}+2 x-3\right) = -(-5)^{2} + 2(-5) - 3 \]

Step 2: Simplify the expression

Calculate each term: \[ -(-5)^{2} = -25 \] \[ 2(-5) = -10 \] \[ -3 = -3 \] Now, combine the terms: \[ -25 - 10 - 3 = -38 \]

Step 3: Conclude the limit

Since the function is a polynomial, the limit exists and is equal to the value obtained by substitution: \[ \lim _{x \rightarrow-5}\left(-x^{2}+2 x-3\right) = -38 \]

The correct choice is: A. $\lim _{x \rightarrow-5}\left(-x^{2}+2 x-3\right) = -38$