Questions: How many pounds of cashews should be mixed with the peanuts to ensure no change in the revenue? The manager buys 80 pounds of cashews and sells the mixture for 3.50 per pound. The manager should mix pounds of cashews with the peanuts.
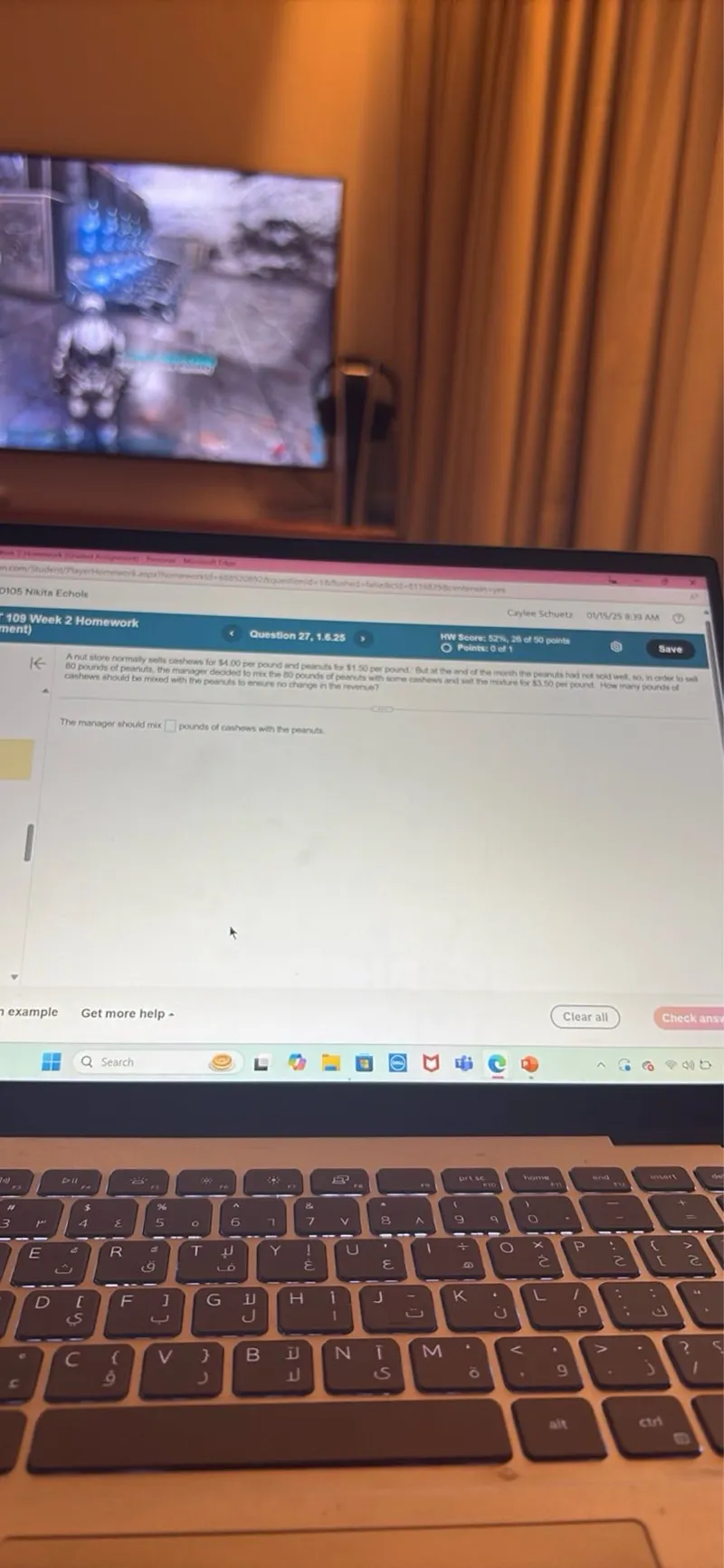
Transcript text: How many pounds of cashews should be mixed with the peanuts to ensure no change in the revenue? The manager buys 80 pounds of cashews and sells the mixture for $3.50 per pound. The manager should mix $\square$ pounds of cashews with the peanuts.





