Questions: Find the expected value of the winnings from a game that has the following payout probability distribution: Payout () -6 -4 -2 0 2 Probability 0.34 0.13 0.06 0.13 0.34 Expected Value = Round to the nearest hundredth.
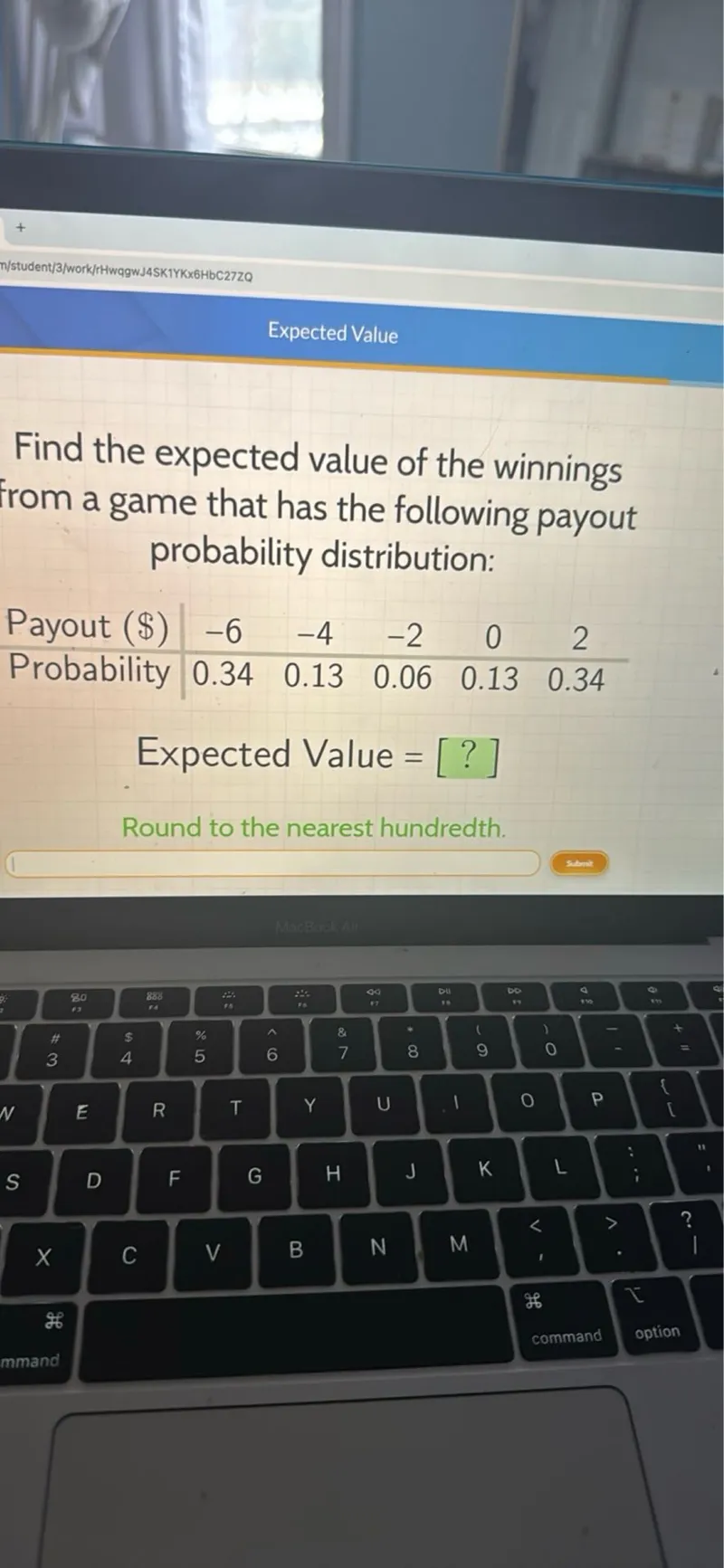
Transcript text: Find the expected value of the winnings from a game that has the following payout probability distribution:
\begin{tabular}{c|ccccc}
Payout (\$) & -6 & -4 & -2 & 0 & 2 \\
\hline Probability & 0.34 & 0.13 & 0.06 & 0.13 & 0.34
\end{tabular}
Expected Value = $\square$
Round to the nearest hundredth.
Solution
Was this solution helpful?
Questions asked by other users
Answered
