Questions: In chemical reactions, heat is converted into chemical energy (the potential energy stored in chemical bonds) or vice versa. Bond energy is the energy required to takes energy to break a bond, bond energies are always positive. Conversely, energy is released when bonds are formed. Thus, the enthalpy change for a reaction can be approximated from ΔHran=Σ(ΔH breaking )+Σ(ΔH forming ) where H represents bond energies for the breaking (positive bond energy) or forming (negative bond energy) of a bond and Hmas represents the overall enthalpy for the reaction. Use the table to answer questions about bond energies. Bond Bond energy (kJ / mol) C-C 347 C=C 611 C-H 414 C-O 360 C=OinCO 799 O-O 142 O=O 498 H-O 464 Calculate the approximate enthalpy change, ΔHmax, for the combustion of one mole of methane as shown in the balanced chemical equation: CH4+2 O2 → 2 H2O+CO2 Use the values you calculated in Parts A, B, C, and D, keeping in mind the stoichiometric coefficients Express your answer to three significant figures and include the appropriate units.

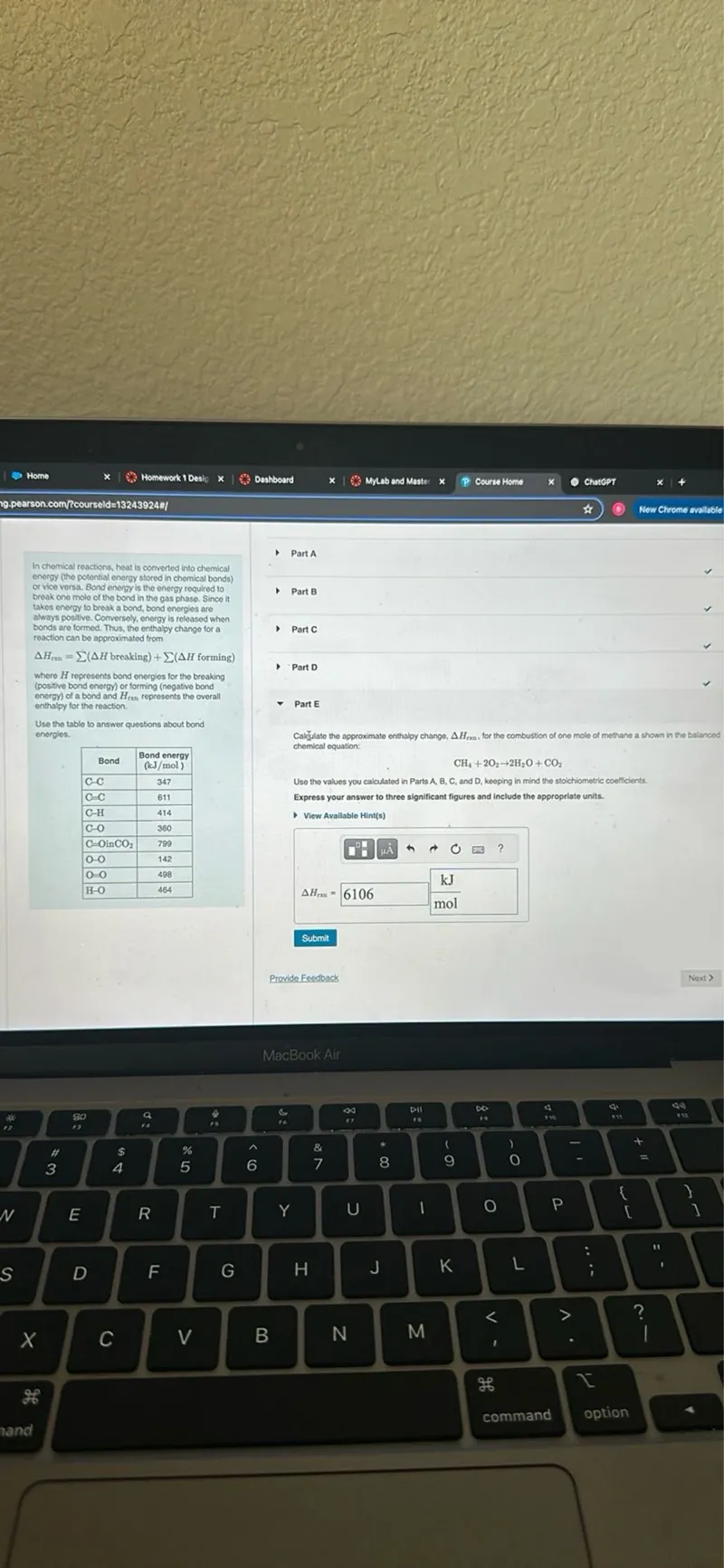
In chemical reactions, heat is converted into chemical energy (the potential energy stored in chemical bonds) or vice versa. Bond energy is the energy required to takes energy to break a bond, bond energies are always positive. Conversely, energy is released when bonds are formed. Thus, the enthalpy change for a reaction can be approximated from ΔHran=Σ(ΔH breaking )+Σ(ΔH forming ) where H represents bond energies for the breaking (positive bond energy) or forming (negative bond energy) of a bond and Hmas represents the overall enthalpy for the reaction. Use the table to answer questions about bond energies. Bond Bond energy (kJ / mol) C-C 347 C=C 611 C-H 414 C-O 360 C=OinCO 799 O-O 142 O=O 498 H-O 464 Calculate the approximate enthalpy change, ΔHmax, for the combustion of one mole of methane as shown in the balanced chemical equation: CH4+2 O2 → 2 H2O+CO2 Use the values you calculated in Parts A, B, C, and D, keeping in mind the stoichiometric coefficients Express your answer to three significant figures and include the appropriate units.
Transcript text: In chemical reactions, heat is converted into chemical energy (the potential energy stored in chemical bonds) or vice versa. Bond energy is the energy required to takes energy to break a bond, bond energies are always positive. Conversely, energy is released when bonds are formed. Thus, the enthalpy change for a reaction can be approximated from $\Delta H_{\mathrm{ran}}=\sum(\Delta H$ breaking $)+\sum(\Delta H$ forming $)$ where $H$ represents bond energies for the breaking (positive bond energy) or forming (negative bond energy) of a bond and $H_{m a s}$ represents the overall enthalpy for the reaction. Use the table to answer questions about bond energies. \begin{tabular}{|l|c|} \hline \multicolumn{1}{|c|}{ Bond } & \begin{tabular}{c} Bond energy \\ $(\mathrm{kJ} / \mathrm{mol})$ \end{tabular} \\ \hline $\mathrm{C}-\mathrm{C}$ & 347 \\ \hline $\mathrm{C}=\mathrm{C}$ & 611 \\ \hline $\mathrm{C}-\mathrm{H}$ & 414 \\ \hline $\mathrm{C}-\mathrm{O}$ & 360 \\ \hline $\mathrm{C}=\mathrm{OinCO}$ & 799 \\ \hline $\mathrm{O}-\mathrm{O}$ & 142 \\ \hline $\mathrm{O}=\mathrm{O}$ & 498 \\ \hline $\mathrm{H}-\mathrm{O}$ & 464 \\ \hline \end{tabular} Calculate the approximate enthalpy change, $\Delta H_{\mathrm{max}}$, for the combustion of one mole of methane as shown in the balanced chemical equation: \[ \mathrm{CH}_{4}+2 \mathrm{O}_{2} \rightarrow 2 \mathrm{H}_{2} \mathrm{O}+\mathrm{CO}_{2} \] Use the values you calculated in Parts A, B, C, and D, keeping in mind the stoichiometric coefficients Express your answer to three significant figures and include the appropriate units.
failed

Solution

failed
failed

Solution Steps

Step 1: Calculate the energy required to break bonds in reactants

The reactants are CH₄ and 2O₂. In CH₄, there are four C-H bonds. The energy required to break these bonds is 4 * 414 kJ/mol = 1656 kJ/mol. In 2O₂, there are two O=O bonds. The energy required to break these bonds is 2 * 498 kJ/mol = 996 kJ/mol.

The total energy required to break the bonds in the reactants is 1656 kJ/mol + 996 kJ/mol = 2652 kJ/mol.

Step 2: Calculate the energy released when bonds are formed in products

The products are 2H₂O and CO₂. In 2H₂O, there are four O-H bonds. The energy released when these bonds are formed is -4 * 464 kJ/mol = -1856 kJ/mol. In CO₂, there are two C=O bonds. The energy released when these bonds are formed is -2 * 799 kJ/mol = -1598 kJ/mol.

The total energy released when the bonds in the products are formed is -1856 kJ/mol + (-1598 kJ/mol) = -3454 kJ/mol.

Step 3: Calculate the enthalpy change for the reaction

The enthalpy change for the reaction (ΔHrxn) is the sum of the energy required to break bonds in reactants and the energy released when bonds are formed in products:

ΔHrxn = 2652 kJ/mol + (-3454 kJ/mol) = -802 kJ/mol

Final Answer

\\(\boxed{-802 \text{ kJ/mol}}\\)

Was this solution helpful?
failed
Unhelpful
failed
Helpful

Questions asked by other users

failedAnswered
(b) (x=y^3+3 y) Make a table of values and sketch the graph of the equation. Find the (x) - and (y)-intercepts. (If an answer does not exist, enter DNE.) (x)-intercept: ((x, y)=(square)) (y)-intercept: ((x, y)=(square)) Test for symmetry. (Select all that apply.)
failedAnswered
Solve the problem. Suppose 14,000 is invested with 3.5% interest for 9 years compounded quarterly. What is the resulting value? 19,157.36 19,182.75 20,005.98 21,233.65
failedAnswered
DCHS Biology CSA Trophic Levels 1 All Bookmarks 12 of 20 12. Producers are primarily responsible for converting sunlight into chemical energy. POSSIBLE POINTS: 1 True False 7 8 9 10 11 12 13 14 15 16 Next English Help Center PRIVACY POLICY Terms of Use PowerSchool © 2024
failedAnswered
Parte de um troféu está sendo projetada computacionalmente a partir da rotação de uma parábola, como pode ser observado nas figuras a seguir. A função real que expressa a parábola é? a) f(x) = –0,25x² – 0,5x + 6 b) f(x) = –0,25x² + 0,5x + 6 c) f(x) =
failedAnswered
An aqueous solution at 25°C has a H3O+ concentration of 7.6 x 10^-8 M. Calculate the OH- concentration. Be sure your answer has the correct number of significant digits.