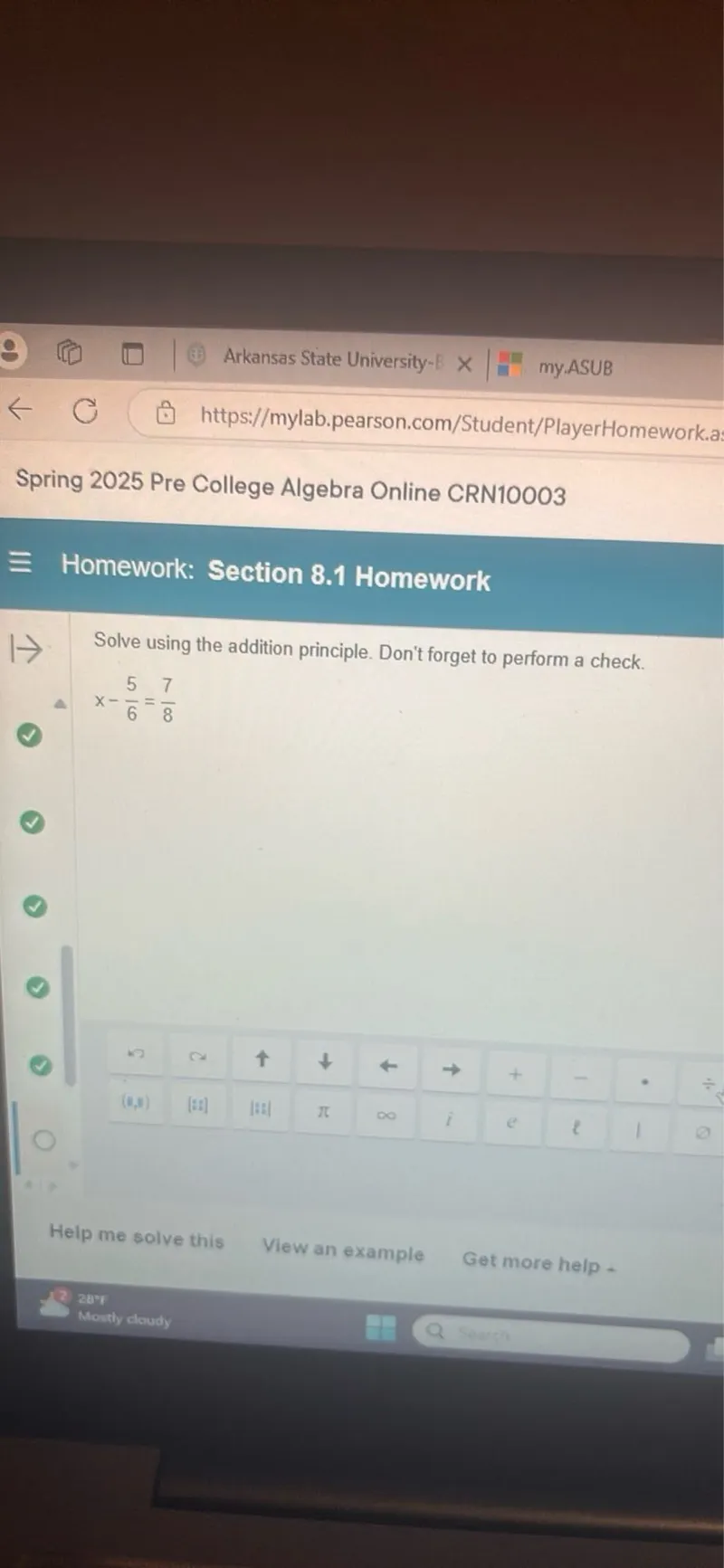
Questions: Solve using the addition principle. Don't forget to perform a check. x - 5/6 = 7/8

Solution Steps

We start with the equation: \[ x - \frac{5}{6} = \frac{7}{8} \]

To isolate \( x \), we add \( \frac{5}{6} \) to both sides of the equation: \[ x = \frac{7}{8} + \frac{5}{6} \]

Next, we need to add the fractions \( \frac{7}{8} \) and \( \frac{5}{6} \). To do this, we find a common denominator. The least common multiple of 8 and 6 is 24. We convert the fractions: \[ \frac{7}{8} = \frac{21}{24} \quad \text{and} \quad \frac{5}{6} = \frac{20}{24} \] Now we can add them: \[ x = \frac{21}{24} + \frac{20}{24} = \frac{41}{24} \]

To verify our solution, we substitute \( x = \frac{41}{24} \) back into the original equation: \[ \frac{41}{24} - \frac{5}{6} \] We convert \( \frac{5}{6} \) to have a common denominator of 24: \[ \frac{5}{6} = \frac{20}{24} \] Now we compute: \[ \frac{41}{24} - \frac{20}{24} = \frac{21}{24} \] We compare this with the right-hand side of the original equation: \[ \frac{7}{8} = \frac{21}{24} \] Since both sides are equal, the check confirms that our solution is correct.

Final Answer