Questions: Tessa wants to buy an antique clock. The sale price is 236. What was the original price?
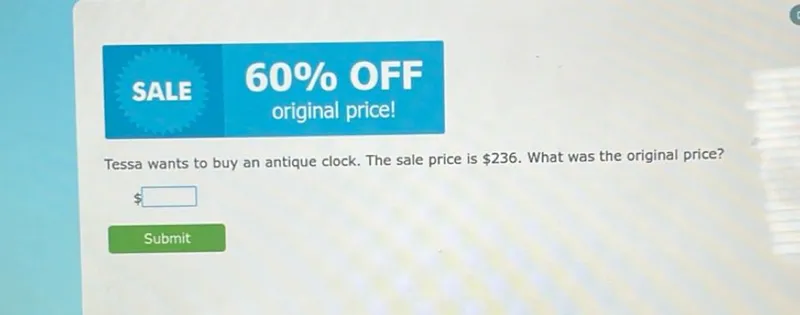
Transcript text: Tessa wants to buy an antique clock. The sale price is $236. What was the original price?





