Questions: Function A Function B y=1/5 x-3 Select all the statements that are true. The y-intercept of Function A is less than the y-intercept of Function B. The y-intercept of Function A is greater than the y-intercept of Function B. The y-value of Function A when x=-10 is equal to the y-value of Function B when x=-10. The y-value of Function A when x=-10 is greater than the y-value of Function B when x=-10.

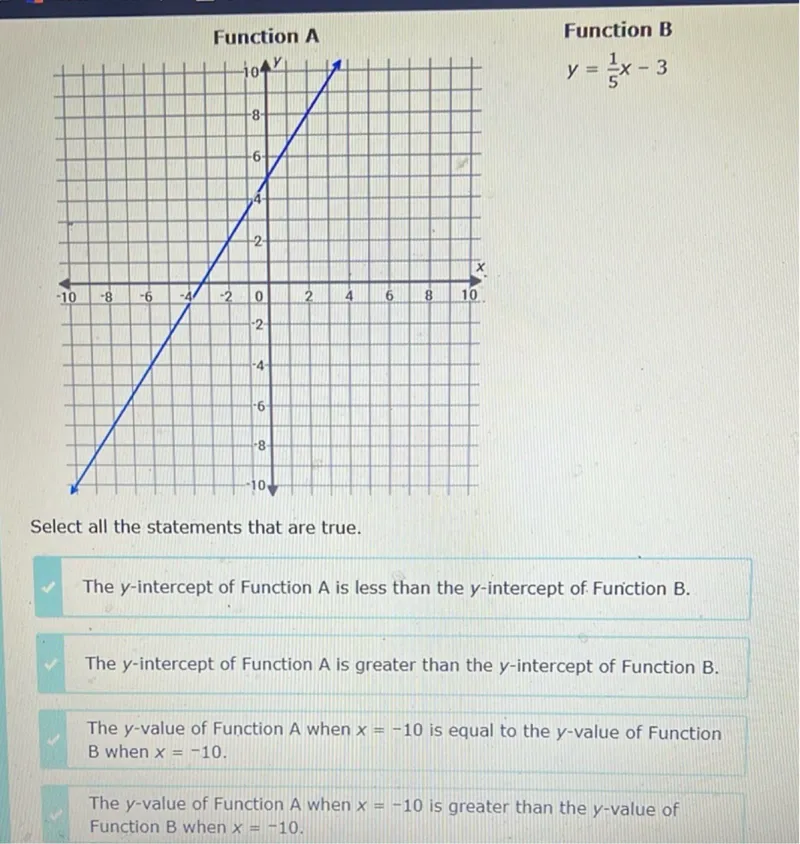
Function A

Function B
y=1/5 x-3

Select all the statements that are true.

The y-intercept of Function A is less than the y-intercept of Function B.

The y-intercept of Function A is greater than the y-intercept of Function B.

The y-value of Function A when x=-10 is equal to the y-value of Function B when x=-10.

The y-value of Function A when x=-10 is greater than the y-value of Function B when x=-10.

Transcript text: Function A Function B \[ y=\frac{1}{5} x-3 \] Select all the statements that are true. The $y$-intercept of Function A is less than the $y$-intercept of Funiction B. The $y$-intercept of Function A is greater than the $y$-intercept of Function B. The $y$-value of Function A when $x=-10$ is equal to the $y$-value of Function B when $x=-10$. The $y$-value of Function A when $x=-10$ is greater than the $y$-value of Function B when $x=-10$.

Solution

Solution Steps

Step 1: Find the y-intercept of Function A.

The y-intercept is the value of y when x = 0. From the graph, we can see that the line representing Function A intersects the y-axis at y = 5. So, the y-intercept of Function A is 5.

Step 2: Find the y-intercept of Function B.

The equation for Function B is given in slope-intercept form: $y = mx + b$, where $m$ is the slope and $b$ is the y-intercept. In this case, $y = \frac{1}{5}x - 3$, so the y-intercept is -3.

Step 3: Compare the y-intercepts.

The y-intercept of Function A is 5, and the y-intercept of Function B is -3. Since 5 > -3, the y-intercept of Function A is greater than the y-intercept of Function B.

Step 4: Find the y-value of Function A when x = -10.

From the graph of Function A, when $x = -10$, $y = -10$.

Step 5: Find the y-value of Function B when x = -10.

Substitute $x = -10$ into the equation for Function B: $y = \frac{1}{5}(-10) - 3 = -2 - 3 = -5$.

Step 6: Compare the y-values when x = -10.

The y-value of Function A when x = -10 is -9, and the y-value of Function B when x = -10 is -5. Since -9 < -5, the y-value of Function A when x = -10 is less than the y-value of Function B when x = -10.

Final Answer

The y-intercept of Function A is greater than the y-intercept of Function B. The y-value of Function A when $x = -10$ is less than the y-value of Function B when $x = -10$.

Was this solution helpful?

Unhelpful

Helpful

Questions asked by other users

< Previous Next >

Thank you for your feedback.

Copied!