Questions: Multiply using the rule for the square of a binomial. (x-10)^2 (x-10)^2=

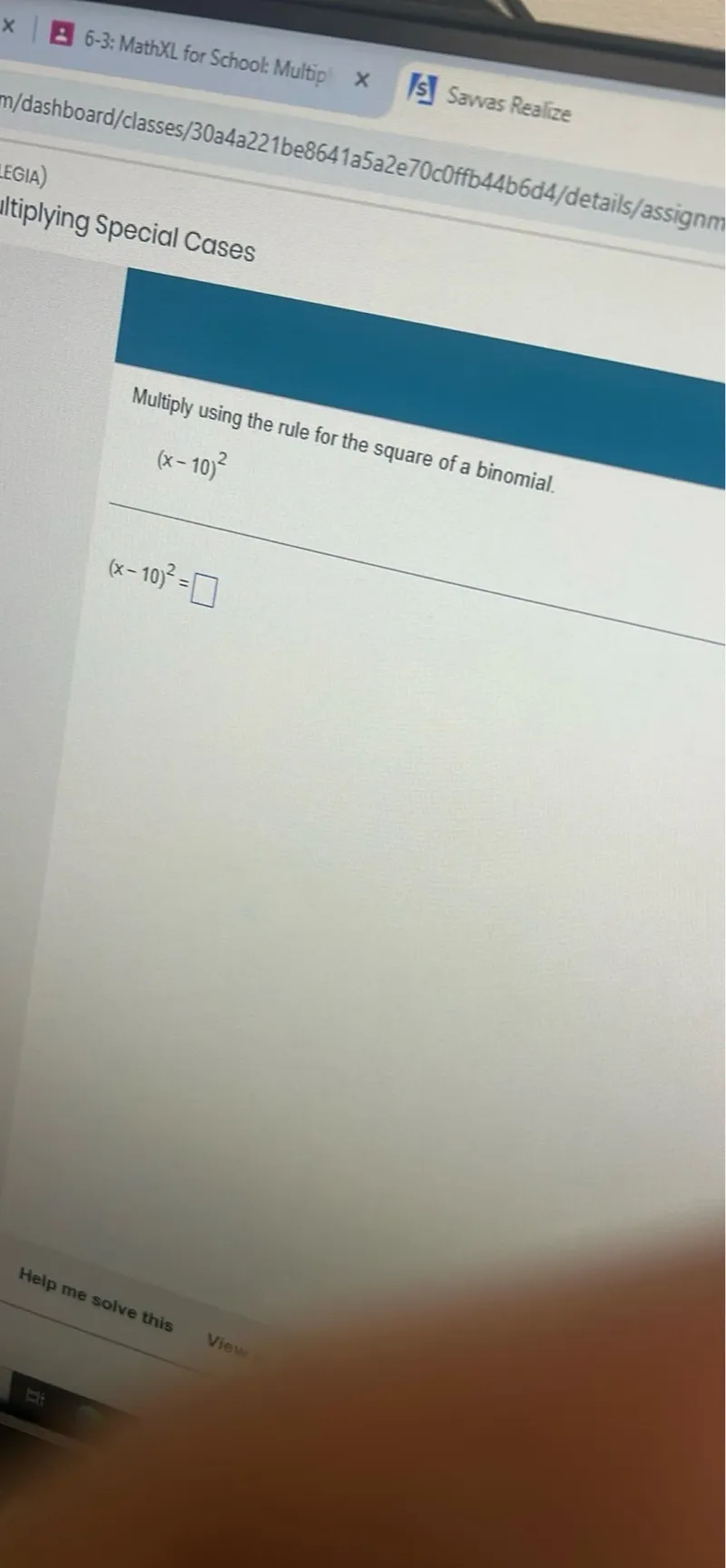
Transcript text: Multiply using the rule for the square of a binomial. \[ (x-10)^{2} \] \[ (x-10)^{2}= \]

Solution

Step 1: Apply the Square of a Binomial Formula

The square of a binomial \((a - b)^2\) is given by the formula: \[ (a - b)^2 = a^2 - 2ab + b^2 \] In this case, \(a = x\) and \(b = 10\).

Step 2: Substitute Values into the Formula

Substitute \(a = x\) and \(b = 10\) into the formula: \[ (x - 10)^2 = x^2 - 2(x)(10) + 10^2 \]

Step 3: Simplify the Expression

Calculate each term:

Combine these results: \[ (x - 10)^2 = x^2 - 20x + 100 \]

\((x - 10)^{2} = \boxed{x^2 - 20x + 100}\)

Was this solution helpful?

Unhelpful

Helpful

Thank you for your feedback.

Copied!