Questions: Question 2: Write a formula for the following polynomial function. You need to show JUSTIFICATION to your answer.

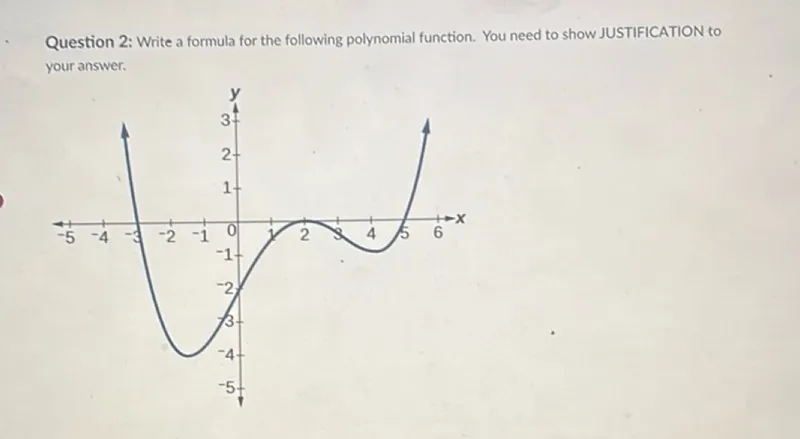
Question 2: Write a formula for the following polynomial function. You need to show JUSTIFICATION to your answer. Find the roots of the polynomial The graph crosses the x-axis at \(x = -3\), \(x = 1\), and \(x = 5\). These are the roots of the polynomial. Determine the multiplicity of each root Since the graph crosses the x-axis at each root, the multiplicity of each root is 1. Write the polynomial in factored form The polynomial can be written in the form \(f(x) = a(x - r_1)(x - r_2)(x - r_3)\), where \(r_1, r_2, r_3\) are the roots, and \(a\) is a constant. Substituting the roots, we have \(f(x) = a(x + 3)(x - 1)(x - 5)\). Find the value of 'a' The graph passes through the point \((0, -2)\). Substituting this into the equation gives \(-2 = a(0 + 3)(0 - 1)(0 - 5)\) \(-2 = 15a\) \(a = -\frac{2}{15}\) Write the final polynomial \(f(x) = -\frac{2}{15}(x+3)(x-1)(x-5)\)

\( \boxed{f(x) = -\frac{2}{15}(x+3)(x-1)(x-5)} \)

\(f(x) = -\frac{2}{15}(x+3)(x-1)(x-5)\)