Questions: A greeting card manufacturer has 400 boxes of a particular card in warehouse I and 270 boxes of the same card in warehouse II. A greeting card shop in San Jose orders 325 boxes of the card, and another shop in Memphis orders 250 boxes. The shipping costs per box to these shops from the two warehouses are shown in the table. How many boxes should be shipped to each city from each warehouse to minimize shipping costs? What is the minimum cost? (Hint: Use x, 325-x, y, and 250-y as the variables.) San Jose Memphis Warehouse I 0.25 0.22 Warehouse II 0.24 0.19 From warehouse I, ship box(es) to San Jose and box(es) to Memphis, and from warehouse II, ship box(es) to San Jose and box(es) to Memphis, for a minimum cost of .
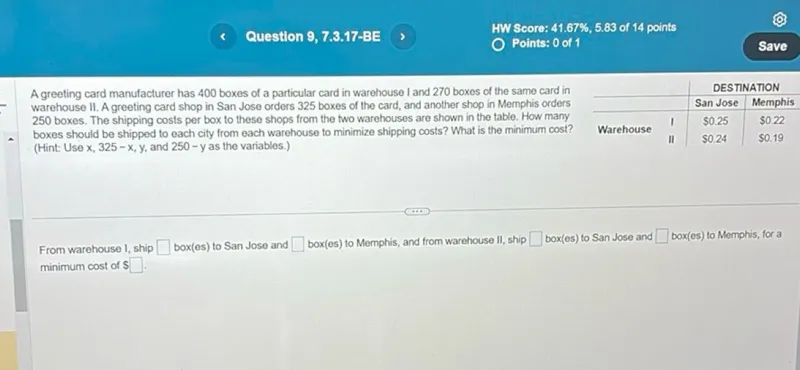
Transcript text: A greeting card manufacturer has 400 boxes of a particular card in warehouse I and 270 boxes of the same card in warehouse II. A greeting card shop in San Jose orders 325 boxes of the card, and another shop in Memphis orders 250 boxes. The shipping costs per box to these shops from the two warehouses are shown in the table. How many boxes should be shipped to each city from each warehouse to minimize shipping costs? What is the minimum cost? (Hint: Use $\mathrm{x}, 325-\mathrm{x}, \mathrm{y}$, and $250-\mathrm{y}$ as the variables.)
\begin{tabular}{cc|c|c}
& & \multicolumn{2}{|c}{ DESTINATION } \\
\hline & San Jose & Memphis \\
\hline \multirow{2}{*}{ Warehouse } & I & $\$ 0.25$ & $\$ 0.22$ \\
& II & $\$ 0.24$ & $\$ 0.19$
\end{tabular}
From warehouse I, ship $\square$ box(es) to San Jose and $\square$ box(es) to Memphis, and from warehouse II, ship $\square$ box(es) to San Jose and $\square$ box(es) to Memphis, for a minimum cost of $\$$ $\square$.





