Questions: Identify the function whose graph appears above. It is either: f(x) = A tan(x) + k or it is f(x) = A cot(x) + k.
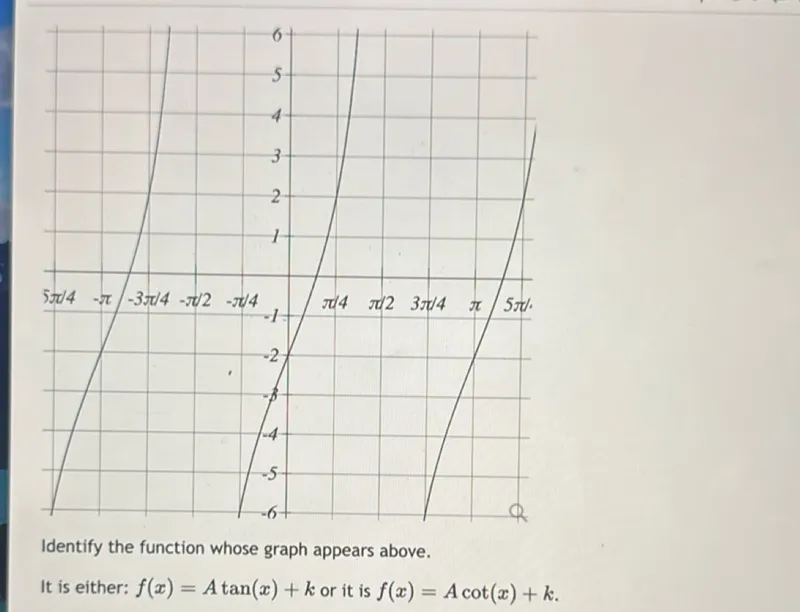
Transcript text: Identify the function whose graph appears above.
It is either: $f(x)=A \tan (x)+k$ or it is $f(x)=A \cot (x)+k$.





