Questions: Applications of Linear Systems: The sum of two integers is 23. If the larger integer is one less than twice the smaller, then find the two integers.

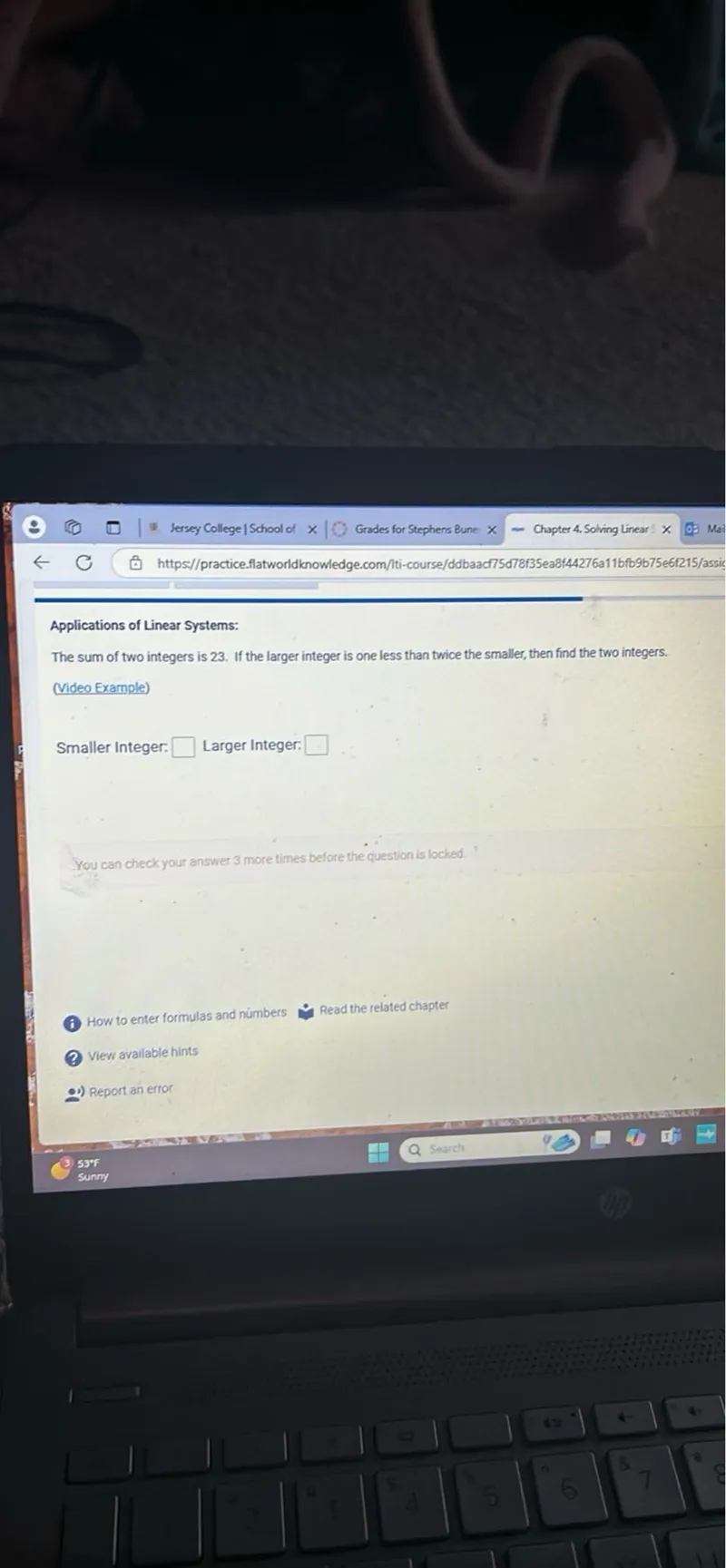
Applications of Linear Systems: The sum of two integers is 23. If the larger integer is one less than twice the smaller, then find the two integers.

Transcript text: Applications of Linear Systems: The sum of two integers is 23. If the larger integer is one less than twice the smaller, then find the two integers.

Solution

Solution Steps

Step 1: Define the Variables

Let \( x \) be the smaller integer and \( y \) be the larger integer.

Step 2: Set Up the Equations

From the problem statement, we have two conditions:

The sum of the two integers is 23: \[ x + y = 23 \]
The larger integer is one less than twice the smaller: \[ y = 2x - 1 \]

Step 3: Substitute and Solve

Substitute the expression for \( y \) from the second equation into the first equation: \[ x + (2x - 1) = 23 \]

Simplify and solve for \( x \): \[ 3x - 1 = 23 \] \[ 3x = 24 \] \[ x = 8 \]

Step 4: Find the Larger Integer

Substitute \( x = 8 \) back into the equation for \( y \): \[ y = 2(8) - 1 = 16 - 1 = 15 \]

Final Answer

Smaller Integer: \(\boxed{8}\)
Larger Integer: \(\boxed{15}\)

Was this solution helpful?

Unhelpful

Helpful

Questions asked by other users

< Previous Next >

Thank you for your feedback.

Copied!