Questions: A typical population curve is shown in the figure. The population is small at t=0 and increases toward a steady-state level called the carrying capacity. The population of a species is given by the function P(t) = K t² / (t² + b), where t ≥ 0 is measured in years and K and b are positive real numbers. Complete parts (a) through (c) below. a. With K=500 and b=18, what is lim t→∞ P(t), the carrying capacity of the population? lim t→∞ P(t) = (Simplify your answer.) b. With K=500 and b=18, when does the maximum growth rate occur? The maximum growth rate occurs at t= . (Type an exact answer, using radicals as needed.) c. For arbitrary values of K and b, when does the maximum growth rate occur (in terms of K and b)? The maximum growth rate occurs at t= . (Type an exact answer, using radicals as needed.)

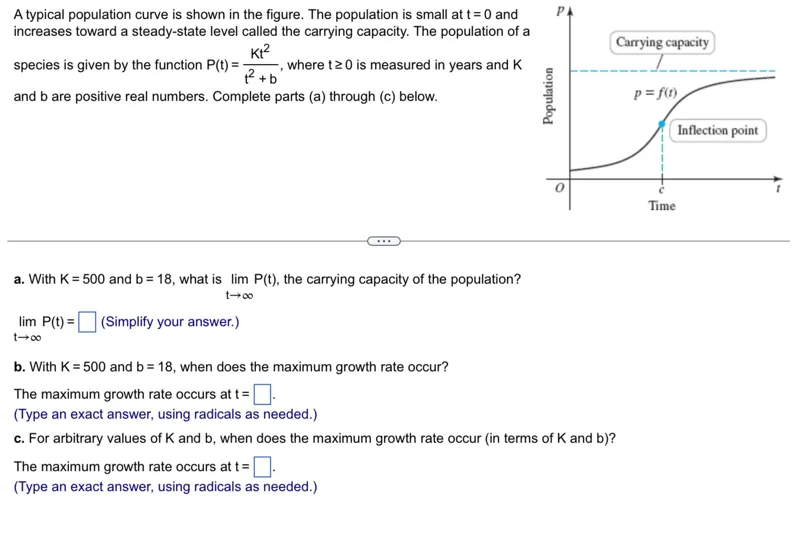
A typical population curve is shown in the figure. The population is small at t=0 and increases toward a steady-state level called the carrying capacity. The population of a species is given by the function P(t) = K t² / (t² + b), where t ≥ 0 is measured in years and K and b are positive real numbers. Complete parts (a) through (c) below.

a. With K=500 and b=18, what is lim t→∞ P(t), the carrying capacity of the population?

lim t→∞ P(t) = (Simplify your answer.)

b. With K=500 and b=18, when does the maximum growth rate occur?

The maximum growth rate occurs at t= .
(Type an exact answer, using radicals as needed.)

c. For arbitrary values of K and b, when does the maximum growth rate occur (in terms of K and b)?

The maximum growth rate occurs at t= .
(Type an exact answer, using radicals as needed.)

Transcript text: A typical population curve is shown in the figure. The population is small at $t=0$ and increases toward a steady-state level called the carrying capacity. The population of a species is given by the function $P(t)=\frac{K t^{2}}{t^{2}+b}$, where $t \geq 0$ is measured in years and $K$ and b are positive real numbers. Complete parts (a) through (c) below. a. With $K=500$ and $b=18$, what is $\lim _{t \rightarrow \infty} P(t)$, the carrying capacity of the population? \[ \lim _{t \rightarrow \infty} P(t)=\square \text { (Simplify your answer.) } \] b. With $K=500$ and $b=18$, when does the maximum growth rate occur? The maximum growth rate occurs at $\mathrm{t}=$ $\square$ . (Type an exact answer, using radicals as needed.) c. For arbitrary values of K and b, when does the maximum growth rate occur (in terms of K and b)? The maximum growth rate occurs at $\mathrm{t}=$ $\square$ . (Type an exact answer, using radicals as needed.)

Solution

Step 1: Determine the limit of P(t) as t approaches infinity

The given function is $ P(t) = \frac{Kt^2}{t^2 + b} $. We need to find $ \lim_{t \to \infty} P(t) $. To evaluate this limit, we can divide both the numerator and the denominator by the highest power of $ t $ in the denominator, which is $ t^2 $: $ \lim_{t \to \infty} P(t) = \lim_{t \to \infty} \frac{\frac{Kt^2}{t^2}}{\frac{t^2}{t^2} + \frac{b}{t^2}} = \lim_{t \to \infty} \frac{K}{1 + \frac{b}{t^2}} $ As $ t \to \infty $, $ \frac{b}{t^2} \to 0 $. Therefore, $ \lim_{t \to \infty} P(t) = \frac{K}{1 + 0} = K $. Given $ K = 500 $ and $ b = 18 $, the carrying capacity is $ K $. So, $ \lim_{t \to \infty} P(t) = 500 $.

Step 2: Find the time of maximum growth rate for specific K and b values

The maximum growth rate occurs at the inflection point of the population curve. This is where the second derivative of $ P(t) $ is equal to zero. First, let's find the first derivative $ P'(t) $, which represents the growth rate. $ P(t) = \frac{Kt^2}{t^2 + b} $ Using the quotient rule $ (\frac{u}{v})' = \frac{u'v - uv'}{v^2} $, where $ u = Kt^2 $ and $ v = t^2 + b $. $ u' = 2Kt $ $ v' = 2t $ $ P'(t) = \frac{(2Kt)(t^2 + b) - (Kt^2)(2t)}{(t^2 + b)^2} $ $ P'(t) = \frac{2Kt^3 + 2Kbt - 2Kt^3}{(t^2 + b)^2} $ $ P'(t) = \frac{2Kbt}{(t^2 + b)^2} $

Now, find the second derivative $ P''(t) $. Let $ u = 2Kbt $ and $ v = (t^2 + b)^2 $. $ u' = 2Kb $ $ v' = 2(t^2 + b)(2t) = 4t(t^2 + b) $ $ P''(t) = \frac{(2Kb)(t^2 + b)^2 - (2Kbt)(4t(t^2 + b))}{((t^2 + b)^2)^2} $ $ P''(t) = \frac{(2Kb)(t^2 + b)^2 - 8Kb t^2 (t^2 + b)}{(t^2 + b)^4} $ Factor out $ 2Kb(t^2 + b) $ from the numerator: $ P''(t) = \frac{2Kb(t^2 + b)[(t^2 + b) - 4t^2]}{(t^2 + b)^4} $ $ P''(t) = \frac{2Kb(t^2 + b - 4t^2)}{(t^2 + b)^3} $ $ P''(t) = \frac{2Kb(b - 3t^2)}{(t^2 + b)^3} $

To find the inflection point, set $ P''(t) = 0 $: $ \frac{2Kb(b - 3t^2)}{(t^2 + b)^3} = 0 $ Since $ K $ and $ b $ are positive, $ 2Kb \neq 0 $. Also, $ (t^2 + b)^3 \neq 0 $ for $ t \ge 0 $. So, we must have $ b - 3t^2 = 0 $. $ 3t^2 = b $ $ t^2 = \frac{b}{3} $ Since $ t \ge 0 $, $ t = \sqrt{\frac{b}{3}} $.

Given $ K = 500 $ and $ b = 18 $: $ t = \sqrt{\frac{18}{3}} = \sqrt{6} $.

Step 3: Find the time of maximum growth rate for arbitrary K and b values

From the previous step, we found that the maximum growth rate occurs at $ t = \sqrt{\frac{b}{3}} $. This expression is already in terms of $ K $ and $ b $, although $ K $ does not appear in the final expression for $ t $.

The final answer is $ \boxed{\text{a. } 500, \text{ b. } \sqrt{6}, \text{ c. } \sqrt{\frac{b}{3}}} $

Was this solution helpful?