Questions: Solve the following logarithmic equation. log5(t+16) - log5(t+7) = log5 t Select the correct choice below and, if necessary, fill in the answer box. A. The solution(s) is/are . (Simplify your answer. Type an integer or a fraction. Use a comma to separate answers as needed.) B. The solution is not a real number.
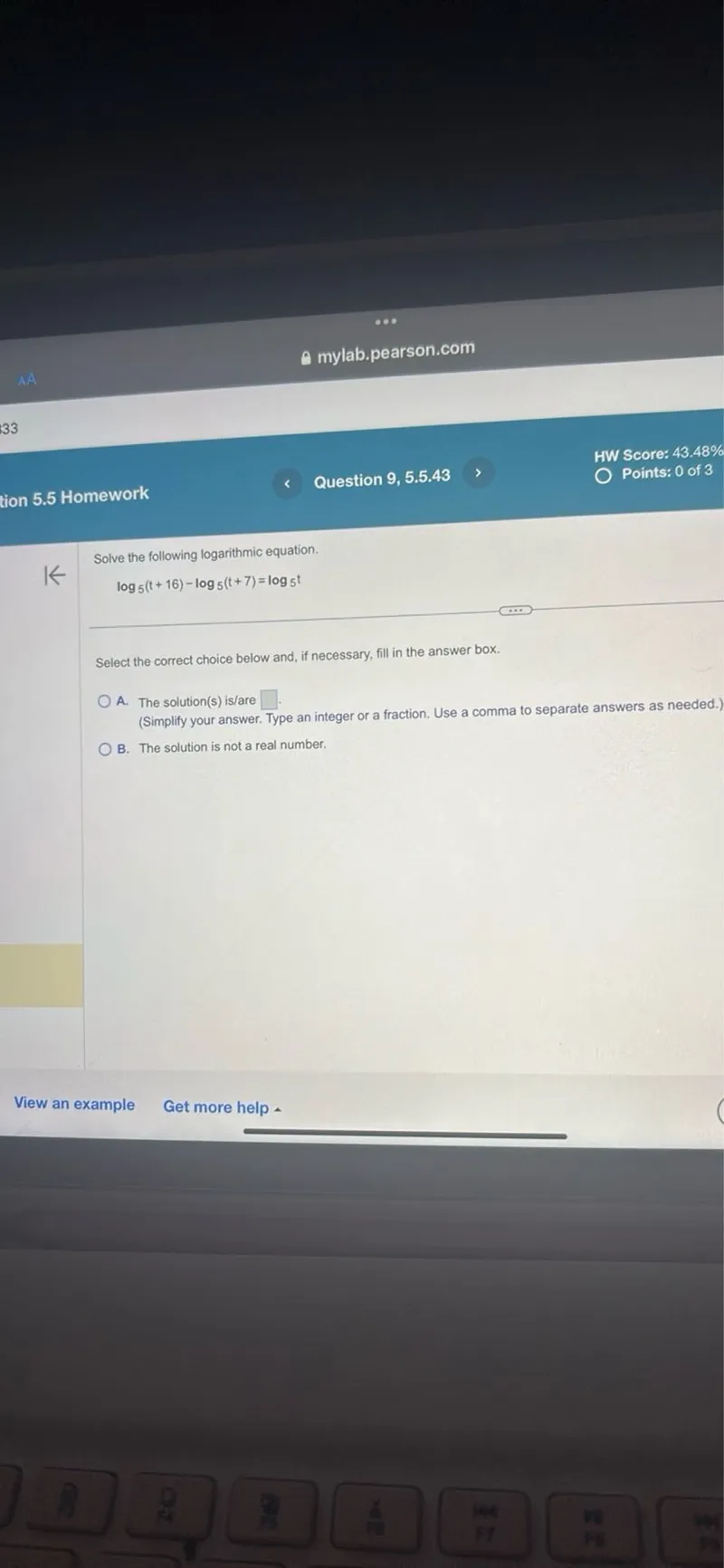
Transcript text: Solve the following logarithmic equation.
\[
\log _{5}(t+16)-\log _{5}(t+7)=\log _{5} t
\]
Select the correct choice below and, if necessary, fill in the answer box.
A. The solution(s) is/are $\square$ $\square$.
(Simplify your answer. Type an integer or a fraction. Use a comma to separate answers as needed.)
B. The solution is not a real number.





