Questions: Question 13 of 25 Select the angle that correctly completes the law of cosines for this triangle. 24^2+25^2-2(24)(25) cos =7^2 A. 90° B. 180° C. 16° D. 74°

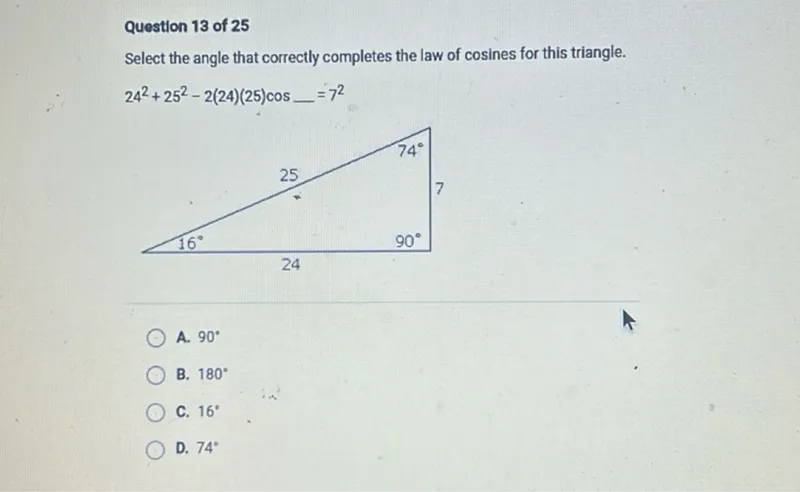
Transcript text: Question 13 of $\mathbf{2 5}$ Select the angle that correctly completes the law of cosines for this triangle. \[ 24^{2}+25^{2}-2(24)(25) \cos \_=7^{2} \] A. $90^{\circ}$ B. $180^{\circ}$ C. $16^{\circ}$ D. $74^{\circ}$

Solution

Solution Steps

Step 1: Identify the sides and angles

The given triangle has sides with lengths 7, 24, and 25. The angles opposite to these sides are $74^\circ$, $16^\circ$, and $90^\circ$ respectively. The law of cosines states that $c^2 = a^2 + b^2 - 2ab \cos(C)$, where $a$, $b$, and $c$ are the sides of the triangle and $C$ is the angle opposite to side $c$.

Step 2: Apply the Law of Cosines

In our case, we are given the equation $24^2 + 25^2 - 2(24)(25)\cos \_ = 7^2$. We can see that the side opposite to the unknown angle is 7. Therefore, the angle we are looking for is the angle opposite the side with length 7.

Step 3: Find the missing angle

From the diagram, the angle opposite to the side with length 7 is $74^\circ$.